Aufgabe:
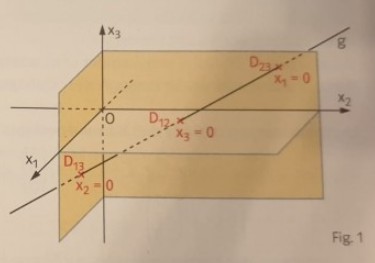
Bestimmen Sie, falls möglich, die Schnittpunkte der Geraden mit den Koordinatenebenen.
a) \( g: \vec{x}=\left(\begin{array}{l}2 \\ 4 \\ 1\end{array}\right)+t \cdot\left(\begin{array}{r}-2 \\ 2 \\ 1\end{array}\right) \)
b) \( g: \vec{x}=\left(\begin{array}{l}2 \\ 2 \\ 2\end{array}\right)+t \cdot\left(\begin{array}{l}1 \\ 3 \\ 0\end{array}\right) \)
Problem/Ansatz:
Ich möchte es schriftlich berechnen. Dachte zuerst man muss die Geradengleichungen gleich setzen.