Hallo,
8i=90°
vermutlich meinst du das richtige, allerdings ist die Schreibweise falsch. Ich würde es so schreiben:
\(z^3=8i=8\cdot e^{i\pi/2}\)
\(|z|=\sqrt[3]8=2\)
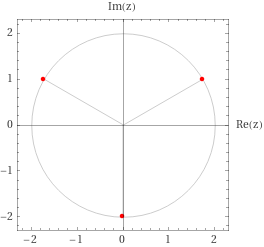
\(\varphi_1=\dfrac13\cdot\dfrac\pi2=\dfrac\pi6\Rightarrow z_1=2\cdot e^{i\pi/6}\)
\(\varphi_2=\varphi_1+\dfrac{2\pi}{3}=\dfrac{5\pi}6\Rightarrow z_2=2\cdot e^{i\cdot5\pi/6}\)
\(\varphi_3=\varphi_1+\dfrac{4\pi}{3}=\dfrac{3\pi}2\Rightarrow z_3=2\cdot e^{i\cdot3\pi/2}\)
Bei Bedarf kannst du das noch in die kartesische Form umwandeln.
PS:
Diese Zeile ist auch falsch:
8*cos(\( \frac{φ+k*2pi}{3} \))+i*sin(\( \frac{φ+k*2pi}{3} \))
Richtig wäre
\(2*(\cos(\frac{\varphi+k*2\pi}{3} )+i*\sin( \frac{\varphi+k*2\pi}{3} ))\)