Bestimmen Sie die Koordinaten des Punktes R und bestimmen Sie eine Gleichung der Ebene E.

Question

Aufgabe:

Die Ebene E schneidet einen Würfel mit der Kantenlänge 10cm. Dabei entsteht das Viereck PQRS.

Bestimmen Sie die Koordinaten des Punktes R und bestimmen Sie eine Gleichung der Ebene E.

Problem/Ansatz:

Ich habe die Gleichung für die Ebene E aufstellen können und habe auch einen Ansatz, um die Koordinaten von R zu bestimmen, doch ich bin der Meinung das ich viel zu kompliziert vorgehe. Denn ich würde, um R herauszufinden die Ebene E mit einer Geraden Gleichsetzen um als Schnittpunkt R herauszubekommen. Meine Gerade hätte in dem Fall den Stützvektor G und den Richtungsvektor (1/0/0) so würde sie die Ebene genau bei R treffen.. Aber ich denke es gibt einen viel simpleren Weg der hier auch gefragt ist.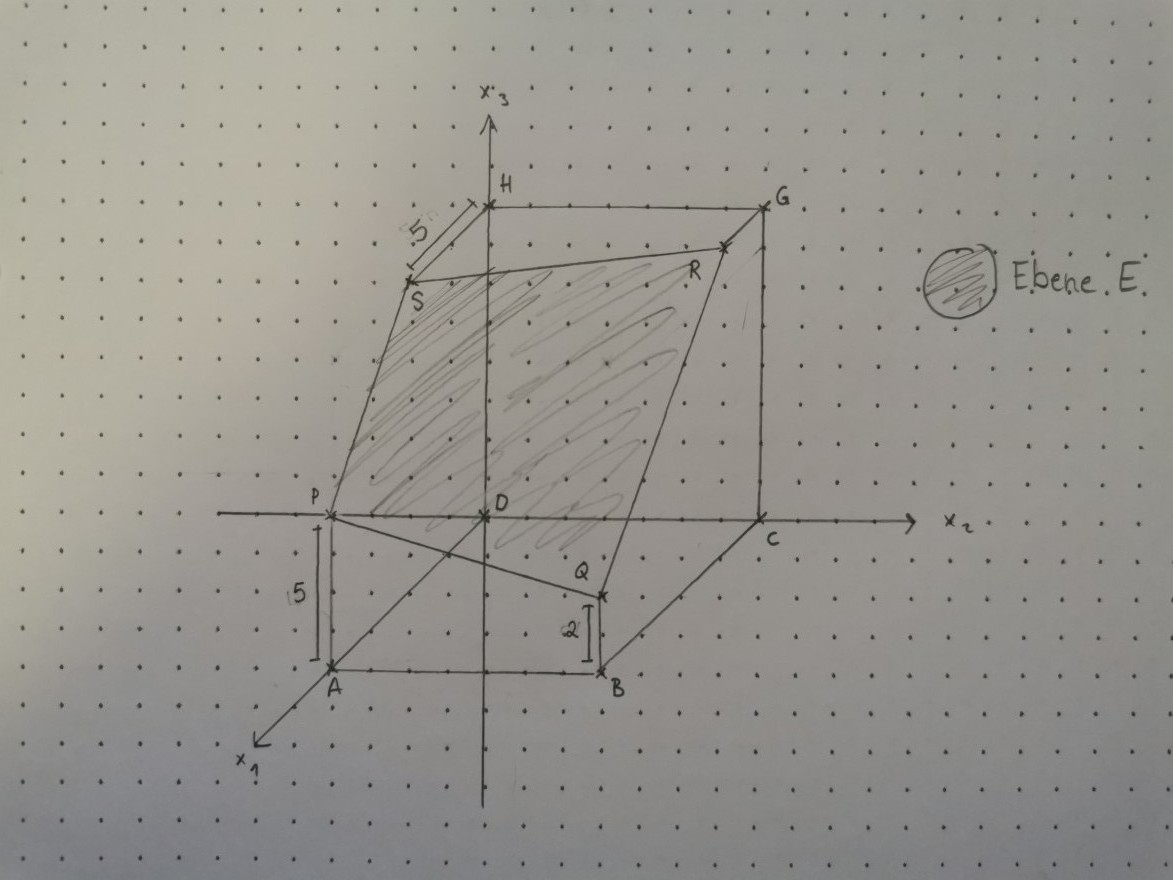

Text erkannt:

Ebene EE.

Answer 1

Aus Symmetriegründen \(\left(\text{i. e. }\left|\vec{AP}\right| = \left|\vec{HS}\right|\right)\) muss \(\left|\vec{GR}\right| = 2\) sein.

der hier auch gefragt ist.

Nein. Es ist gefragt, dass du aufgrund von mathematisch korrekten Überlegungen zu einer mathematisch korrekten Lösung kommst. Extrapunkte für die eleganteste Lösung gibt es nicht.

Der einfachere Rechenweg ist lediglich dahingehend klausurrelevant, dass er Zeit spart.

Comments

Mein Gedanke dabei war, dass die Länge des Vektors GR ja theoretisch auch 1,9 sein könnte. Welche Symmetriegründe erklären denn, dass es 2 sein muss?

---

Ich weiß ja jetzt nicht, ob du schon

\(\left(\text{i. e. }\left|\vec{AP}\right| = \left|\vec{HS}\right|\right)\)

gelesen hast. Das hatte ich später hinzugefügt.

---

Nein das hatte ich bis eben noch nicht gelesen, aber vielen Dank, das hat mir sehr geholfen!
Und ja du hast recht, dass es in der Regel nicht darauf ankommt wie man zum Ergebnis kommt, solange es stimmt. Aber meine Überlegung kam mir schon sehr aufwendig vor und ich wollte gerne einen simpleren Weg kennen :) Also vielen Dank nochmal für die schnelle Antwort!