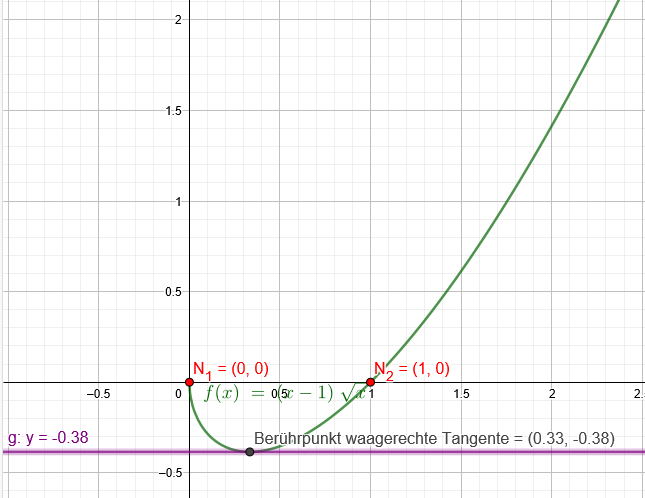
Gegeben ist die Funktion f mit f(x) = (x-1)•\( \sqrt{x} \)
a) Bestimmen sie die Schnittpunkte des Graphen von f mit der x-Achse
(x-1)•\( \sqrt{x} \)=0
x₁=1
x₂=0
b) Welche Steigung hat die Tangente an den Graphen im Punkt P(1|f(1))?
\( f^{\prime}(x)=\sqrt{x}+\frac{x-1}{2 \sqrt{x}} \)
\( f^{\prime}(1)=\sqrt{1}=1 \)
c) In welchen Punkten hat der Graph von \( f \) waagerechte Tangenten?
\( \sqrt{x}+\frac{x-1}{2 \sqrt{x}}=0 \mid \cdot 2 \sqrt{x} \)
\( 2 x+x-1=0 \)
\( x=\frac{1}{3} \rightarrow f\left(\frac{1}{3}\right)=\left(\frac{1}{3}-1\right) \cdot \sqrt{\frac{1}{3}} \approx-0,4 \)