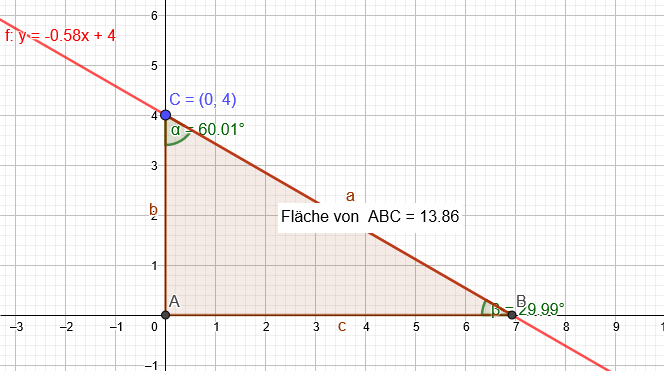
Im rechtwinkligen Dreieck ABC mit α=90° betragen der Kathetenlänge AC=4cm und der Flächeninhalt ist 13,86cm^2. Berechne die Innenwinkelmaße.
Gerade durch C:
y=m*x+4
Nullstelle: m*x+4=0 → x=-\( \frac{4}{m} \)
\( 13,86=\int \limits_{0}^{-\frac{4}{m}}(m x+4) \cdot d x=\left[\frac{m}{2} \cdot x^{2}+4 x\right]_{0}^{-\frac{4}{m}}=\left[\frac{m}{2} \cdot\left(-\frac{4}{m}\right)^{2}+4 \cdot\left(-\frac{4}{m}\right)\right]-0=-\frac{8}{m} \)
\( m \approx-0,577201 \)
\( \tan ^{-1}(-0,577201) \approx 29,99 \circ \)
\( \beta=29,99 \circ \) und \( \gamma=60,01^{\circ} \)