Bestimmen Sie eine geeignete ganzrationale Funktion mit möglichst geringem Grad.

Question

Aufgabe:

Das rosa gefärbte Kunststoffteil der Rutsche beginnt und endet jeweils waagerecht. a) Bestimmen Sie eine geeignete ganzrationale Funktion mit möglichst geringem Grad. b) Berechnen Sie mit dem Ergebnis aus a) die Stelle, an der die Rutsche am steilsten ist, und geben Sie diese Steigung

Problem/Ansatz:

Kann jemand mir dabei bitte helfen

Comments

In der Abbildung fast nicht sichtbar. Die Rutsche ist 1 m hoch und in der Draufsicht 1,5 m lang.

Answer 1

Für zwei lokale Extremstellen (Steigung Null) braucht es eine kubische Funktion.

Wenn der Ursprung des Koordinatensystems am unteren Ende der Rutsche ist, dann lautet das Gleichungssystem der Steckbriefaufgabe (in cm):

\( a \cdot 0^{3}+b \cdot 0^{2}+c \cdot 0+d=0 \)                              unteres Ende

\(3 a \cdot 0^{2}+2 b \cdot 0+c=0 \)                                         ... ist waagerecht

\( a \cdot 150^{3}+b \cdot 150^{2}+c \cdot 150+d=100\)             oberes Ende

\(3 a \cdot 150^{2}+2 b \cdot150+c=0 \)                                 ... ist waagerecht

mit der Lösung

\( a=-\frac{1}{16875}, \quad b=\frac{1}{75}, \quad c=0, \quad d=0 \)

Die Funktion ist also \( y=-\frac{1}{16875} x^{3} + \frac{1}{75} x^{2} \)

Comments

Die Rutsche:

Answer 2

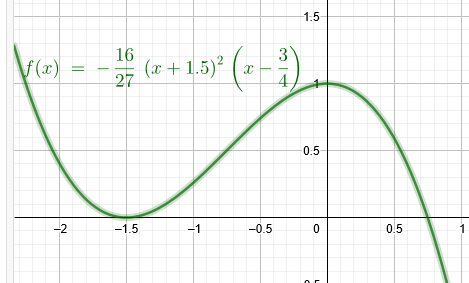
Lösung über die Nullstellenform der Parabel 3.Grades:

doppelte Nullstelle bei P(-1,5|0)

f(x)=a*(x+1,5)^2*(x-N)

Q(0|1):

f(0)=a*(0+1,5)^2*(0-N)=-2,25aN

1.)-2,25aN=1   → a=-\( \frac{1}{2,25N} \)

Extremwert bei Q(0|1):

f(x)=-\( \frac{1}{2,25N} \)*(x+1,5)^2*(x-N)

f´(x)=-\( \frac{1}{2,25N} \)[2*(x+1,5)(x-N)+(x+1,5)^2*1]

f´(0)=-\( \frac{1}{2,25N} \)[2*(0+1,5)(0-N)+(0+1,5)^2]

-\( \frac{1}{2,25N} \)[3*(-N)+2,25]=0

N≈\( \frac{3}{4} \)     a=-\( \frac{1}{2,25*0,75} \)    a=-\( \frac{16}{27} \)

f(x)=-\( \frac{16}{27} \)*(x+1,5)^2*(x-\( \frac{3}{4} \) )