Kann mir jemand den mittleren Schritt erläutern? Wie kommt man von \( \sum\limits_{n=1}^{n}{} \) log(\( \frac{k+1}{k} \)) auf \( \sum\limits_{k=1}^{n}{} \) log(1+ k) - \( \sum\limits_{k = 0}^{n-1}{} \) log(1+ k)
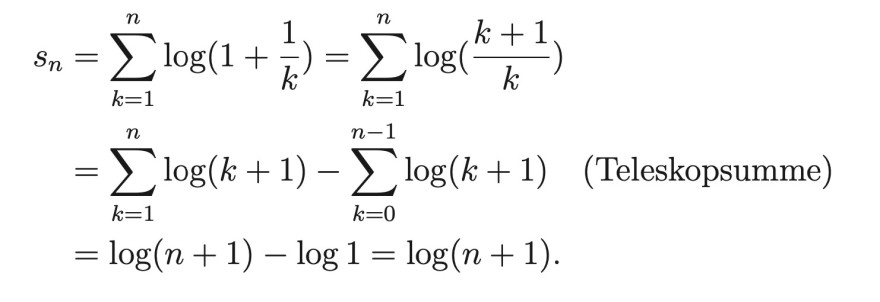
Text erkannt:
\( \begin{aligned} s_{n} &=\sum \limits_{k=1}^{n} \log \left(1+\frac{1}{k}\right)=\sum \limits_{k=1}^{n} \log \left(\frac{k+1}{k}\right) \\ &=\sum \limits_{k=1}^{n} \log (k+1)-\sum \limits_{k=0}^{n-1} \log (k+1) \quad \text { (Teleskopsumme) } \\ &=\log (n+1)-\log 1=\log (n+1) \end{aligned} \)
Vielen Dank!