Hier eine Skizze
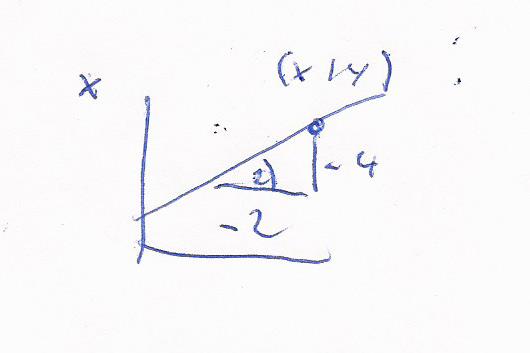 Angenommen wird ein Punkt ( x | y )
Angenommen wird ein Punkt ( x | y )
Wenn x um 2 reduziert wird wird y um 4 Reduziert.
Das Steigungsdreieck zeigt delta y / delta x = -4 / -2 = 2
Die Steigung ist 2
Geradengleichung
f ( x ) = 2 * x + b
b kann willkürlich gewählt werden. Siehe die Antwort von Roland.
b) Bestimmen Sie die Stelle, an der die lineare Funktion f mit
f(3) - 7 und f(8) - 10 den Wert -6 annimmt.
Meinst du
f ( x ) = 2 * x + b
f ( 3 ) = 2 * 3 + b
f ( 3 ) - 7 = 2 * 3 + b -7
f ( 8 ) = 2 * 8 + b
f ( 8 ) - 10 = 2 * 8 + b - 10
2 * 3 + b -7 minus ( 2 * 8 + b - 10 ) = -6
Gibt leider nichts.