Reihenwert berechnen mit Indexverschiebung

Question

Aufgabe:

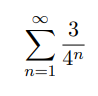
Problem/Ansatz:

Hallo!

Bei dieser Aufgabe soll man den Wert der Reihe berechnen und dazu gab es auch irgendwie eine Lösung, die ich allerdings nicht ganz verstehe:

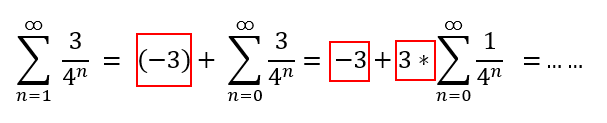
Woher kommen die ganzen rot markierten Zahlen her? Ich weiß, dass es etwas mit der Indexverschiebung zu tun hat... Aber wie genau funktioniert das? Kann mir das jemand ganz kurz erklären?

Answer 1

Aloha :)

Da ist zuerst eine "nahrhafte Null" addiert worden:$$\sum\limits_{n=1}^\infty\frac{3}{4^n}=\underbrace{\left(-3+\frac{3}{4^0}\right)}_{=0}+\sum\limits_{n=1}^\infty\frac{3}{4^{n}}=-3+\left(\frac{3}{4^0}+\sum\limits_{n=1}^\infty\frac{3}{4^{n}}\right)=-3+\sum\limits_{n=0}^\infty\frac{3}{4^{n}}$$Anschließend wurde der konstante Faktor \(3\) aus den Summanden herausgezogen:$$=-3+\sum\limits_{n=0}^\infty\frac{3}{4^{n}}=-3+3\sum\limits_{n=0}^\infty\frac{1}{4^{n}}$$Danach kann man mit der geometrischen Reihe den Wert der Summe bestimmen:$$=-3+3\sum\limits_{n=0}^\infty\left(\frac14\right)^n=-3+3\cdot\frac{1}{1-\frac{1}{4}}=-3+3\cdot\frac{1}{\frac34}=-3+4=1$$

Comments

Und -3 kommt von wo genau her?

Danke für die super ausführliche Antwort übrigens!

---

Da der Index bei n=0 anfangen soll statt bei n=1 rechnest du den Wert für n=0 aus, also 3/4^0=3/1=3.

Wenn die Summe nun bei n=0 beginnt, ist das Ergebnis um 3 zu groß. Deshalb addierst du -3.

:-)

---

Aso, na dann. Vielen Dank für die Antwort! ;-)

Answer 2

Ohne Indexverschiebung geht es direkt:

a0= 3/4

q= 1/4

-> Summe = (3/4)/(1-1/4) = 3/4*4/3= 1

Comments

Hätte auch funktioniert, stimmt. Danke für den Hinweis! :-)