Aufgabe:
sind das V und O richtig?
V= 3 * 4 * 4 = 48 cm^3
O = links + rechte = 2 * (4 * 5) = 40
Unten und oben 2 (*5 * 4 )= 40
Vorne und hinten 2 * ( 5* 1 + 2 * [ 1 *4] )= 26
von Innen 2 * 4 * 4= 32
O = 40 + 40 +26+32 = 138 cm ^2 . Stimmt meine Lösung?
Im Buch aber anders
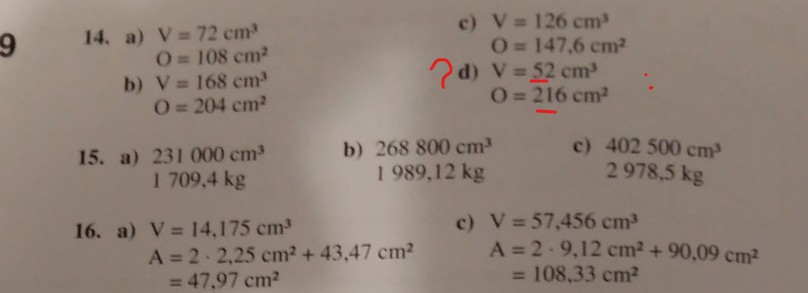
Text erkannt:
14. a) \( V=72 \mathrm{~cm}^{3} \)
c) \( \mathrm{V}=126 \mathrm{~cm}^{3} \)
\( \mathrm{O}=108 \mathrm{~cm}^{2} \)
b) \( V=168 \mathrm{~cm}^{3} \)
\( \ldots . . .6 \mathrm{~cm}^{2} \)
\( \mathrm{O}=204 \mathrm{~cm}^{2} \)
d) \( \begin{aligned} \mathrm{V} &=52 \mathrm{~cm}^{3} \\ \mathrm{O} &=216 \mathrm{~cm}^{2} \end{aligned} \)
15. a) \( 231000 \mathrm{~cm}^{3} \)
b) \( 268800 \mathrm{~cm}^{3} \) \( 1989,12 \mathrm{~kg} \)
c) \( 402500 \mathrm{~cm}^{3} \)
16. a)
\( \begin{aligned} \mathrm{V} &=14,175 \mathrm{~cm}^{3} \\ \mathrm{~A} &=2 \cdot 2,25 \mathrm{~cm}^{2}+43,47 \mathrm{~cm}^{2} \\ &=47,97 \mathrm{~cm}^{2} \end{aligned} \)
\( \text { c) } \mathrm{V}=57,456 \mathrm{~cm}^{3} \)
Text erkannt:
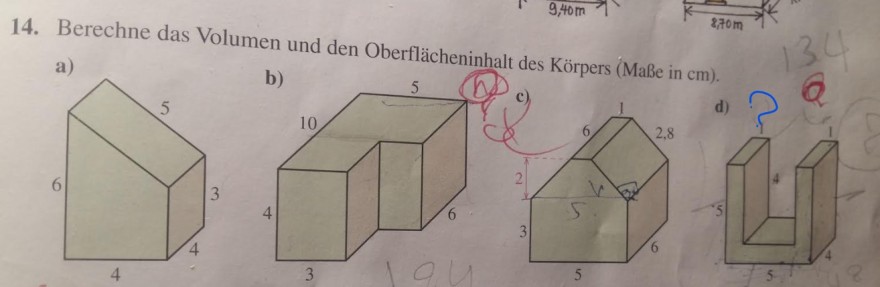
14. Berechne das Volumen und den Oberflächeninhalt des Körpers (Maße in cm).
b)