Tangente mit Schnittaufgabe

Question

Hallo, kann mir bitte jemand mit diesem Beispiel helfen?

Ermittle jene Tangente an die Parabel par, die zur Geraden g normal ist. Gib auch die Koordinaten des Berührpunktes an.

g: A=(0|2), B=(2|0)

Par: y²=8x

Danke vielmals im Voraus

Comments

Falls es interessiert:

Die geometrische Lösung sieht so aus. Eine Parabel sei gegeben durch ihren Brennpunkt $F$ und die Leitgerade $l$ (blau gestrichelt). Man zeichnet eine Parallele (lila) zu $g$ (rot) durch $F$, die $l$ in $Q$ schneidet. Die Mittelsenkrechte der Strecke $FQ$ ist die gesuchte Tangente $t$ (grün).

Der Berührpunkt $B$ ist der Schnittpunkt von $t$ und der Orthogonalen zu $l$ durch $Q$.

https://jsfiddle.net/WernerSalomon/ng25e4kt/28/

man kann die Punkte $F$, $G$ und $A$ verschieben und die Steigung von $l$ und $g$ mit der Maus verändern.

Answer 1

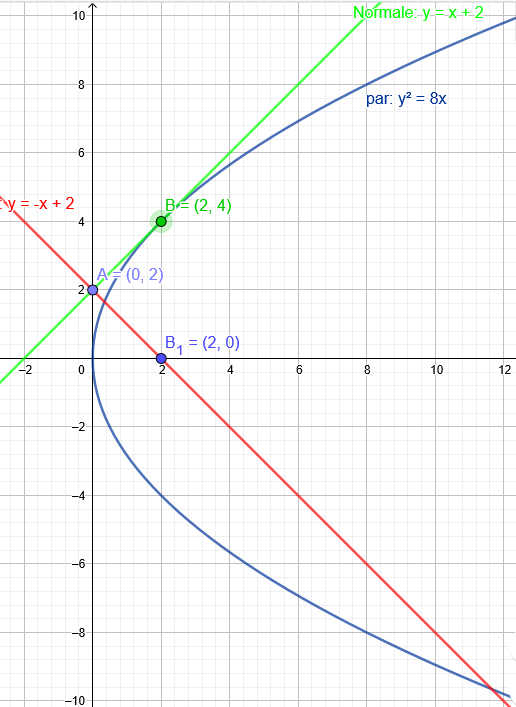
Ermittle jene Tangente an die Parabel par, die zur Geraden g normal ist. Gib auch die Koordinaten des Berührpunktes an.
g: A=(0|2), B=(2|0)    Par: y²=8x

Gerade  g(x)=-x+2     m₁=-1

Normalensteigung  m₂ =1

Normale: y=x+b  schneiden mit y²=8x

(x+b)²=8x

x²+2bx+b²=8x

x²+x*(2b-8)=-b²

(x+b-4)^2=-b^2+b^2-8b+16=16-8b |$\sqrt{}$

16-8b=0

b=2

Normale: y=x+2

Berührpunkt:

x+b-4=0     x+2-4=0    x=2     y=2+2=4

B(2|4)

Comments

@Moliets: verwendest Du den Graphikrechner von desmos.com für die Bilder?

---

Nein, ich nehme für die Darstellung GeoGebra.

Answer 2

g(x) = mx+b

m= (0-2)/(2-0) = -1

2= -1*0+b

b= 2

g(x)= -x+2

...

Answer 3

Die Steigung der geraden ist -1. Damit ist die steigung der Normalen 1. Die Ableitung der Parabelfunktion muss gleich 1 sein.

y=√(8x)

y'=1/(2*√(8x)*8=4/√(8x)=4/(2*√(2x)=2/√(2x)=1 mit Kettenregel

2=√(2x)

4=2x

x=2

Berührpunkt

y=√(8*2)=√16=4

B(2/4)

Normale

y=x+b  Berührpunkt einsetzen

4=2+b

b=2

Normale: y=x+2