Tangente herausfinden und die Koordinaten des Punkt P?

Question

Aufgabe

Skizziere im Koordinatensystem die Gerade g(x)=2x     und den Graphen   von f(x)=2/x

b) P (u/v) liegt auf dem Graphen von f im 1. Quadranten (u ist nicht gleich 1!). Ermittle die Gleichung der Kurventangente in P (in Abhängigkeit von u).

c) Diese Tangente schneidet die Gerade g in Q und die x-Achse R. Das Dreieck ORQ (o gleich Ursprung)) hat den Flächeninhalt A = 3.6. Welche Koordinaten hat der Punkt P in diesem Fall?

Problem:

25 b habe ich einigermassen herausbekommen  --->t(x)= -(2/x^2) *x + 4x^-1

Aber in der Lösung steht → t(x) = -(2/u^2) * x + 4/u       wie sind sie auf das gekommen? Und geht mein Resultat auch?

bei 25 c habe ich überhaupt keine Ahnung. Eigentlich sollte ich ja die Tangente und die Gerade gleichstellen, aber ich bin irgendwie auf 2=2 gekommen oder so.

Answer 1

Tangentengleichung yt=ft(x)=f´(xo)*(x-xo)+f(xo)  mit xo=u

xo=Stelle,wo die Tangente an der Funktion f(x)=2/x liegen soll

abgeleitet f´(x)=1*x^(-1-1)*(-1)=-2/x²

ft(x)=(-2/u²)*(x-u)+2/u=(-2/u²)*x+2*u/u²+2/u=(-2/u²)*x+2/u+2/u

Tangentengleichung yt=ft(x)=-2/u²*x+4/u

Hinweis: g(x)=2*x und f(x)=2/x schneiden sich im Punkt x1=-1 und x2=1

gleichgesetzt 2*x=-2/u²*x+4/u  → Punkt Q

0=-2/u²*x+4/u  →  R

Weiter weiß ich auch nicht ohne Zeichnung und Proberechnungen

setze mal P(1,2/v)  also u=1,2 und mach mal eine komplette Rechnung

zeichne auch die beiden Funktionen auf Millimeterpapier und dann kannst du die Flächen auszählen

Ich werde die Aufgabe mal in meine Aufgabensammlung aufnehmen und komplett durchrechnen

Comments

Danke schön übrigens. Ich habe es heute noch einmal versucht und konnte es schlussendlich ausrechnen.

Ich musste R herausfinden und dies machte ich in dem y 0 ist und r als x ersetze. r gibt dann 2u

danach muss ich noch q herausfinden.

also 2x=t(x)  (ich mag es nicht ganz aufschreiben, dauert zu lange). Wenn ich das herausgerechnet habe, habe ich somit x aber ich brauche ja y um die Fläche zu bekommen. Also x in bei  t(x) als x einsetzen. somit bekomme ich als y= (4u)/(u^2+1)

und ich weiss, dass( y * r )/2 gleich die Flcäeh 3.6 ist

also ((4u)/(u^2+1)) * 2u   und dann das ganze geteilt durch 2 = 3.6

dann nach u auflösen

---

Problem bei solchen Aufgaben ist,dass sie unübersichtlich sind und viel Rechnerei erfordern.

1) immer eine Zeichnung mache,auf Millimeterpapier.Da kann man den Flächeninhalt auszählen.

2) Zur Sicherheit eine Proberechnung durchführen mit ganzen Zahlen,mit denen man gut rechnen kann.

Problem bei mir ist,dass ich nicht bezahlt werde und für solch eine Aufgabe brauche ich mindestens 30 Minuten,wenn ich die komplett durchrechnen muß

---

ja, die hab ich auch gebraucht-.-   Keine Ahnung wie ich die mündliche Prüfung in 15 min lösen sollte.

Answer 2

Hallo,

Aber in der Lösung steht → t(x) = -(2/u²) * x + 4/u      wie sind sie auf das gekommen?

genau wie Du - nur dass sie das \(u\) nicht durch das \(x\) ersetzt haben.

habe ich einigermassen herausbekommen  --->t(x)= -(2/x²) *x + 4x^-1
Und geht mein Resultat auch?

Nein - das ist ja keine Gerade. Sondern da steht ja \(t(x) = - \frac {2x}{x^2} + \frac 4x = \frac 2x\). Irgendwann hast Du in Deiner Rechnung aus dem \(u \) ein \(x\) gemacht. Das ist aber nicht dasselbe.

Diese Tangente schneidet die Gerade g in Q und die x-Achse R. Das Dreieck ORQ (o gleich Ursprung)) hat den Flächeninhalt A = 3.6. Welche Koordinaten hat der Punkt P in diesem Fall?

Die Tangente ist das \(t(x)\) von oben und \(g\) ist gegeben. $$t(x) = -\frac2{u^{2}} \cdot x + \frac 4u \\ g: \space y=2x$$Setze beides gleich um die X-Koordinate \(x_Q\) von \(Q\) zu berechnen:$$  \begin{aligned} 2x_Q &= -\frac2{u^{2}} \cdot x_Q + \frac 4u \\ 2u^2x_Q + 2x_Q &= 4u\\ x_Q &= \frac{2u}{u^2 + 1} ; \quad \implies y_Q = 2x_Q = \frac{4u}{u^2 + 1} \end{aligned}$$\(R\) ist der Schnittpunkt der Tangente \(t(x)\) mit der X-Achse. Dort ist \(y_R=0\) also$$R(0;\, x_R): \space t(x_R)=0 \implies x_R = \frac{4u}{2} = 2u$$

Schau Dir folgendes Applet an. Dort findest Du das Dreieck \(\triangle ORQ\)

https://jsfiddle.net/WernerSalomon/sedq10fx/6/

Leider habe ich es nicht hinbekommen, die Hyperbel sichtbar zu machen. Der Punkt \(P\) liegt immer auf der Hyperbel \(f(x)=2/x\). Daher hier noch mal ein Bild:

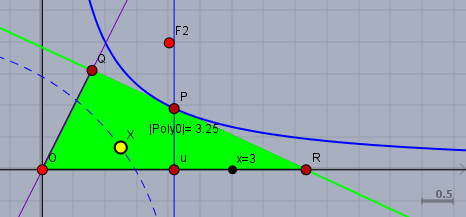
Wenn Du oben im Applet den Punkt \(X\) mit der Maus auf der Kreisbahn verschiebst, so kannst Du sehen, wie sich das Dreieck verändert.

Seine Höhe ist \(y_Q\) und die Länge der Grundseite ist \(x_R\). Folglich ist seine Fläche$$A_{ORQ} = \frac 12 y_Q \cdot x_R = \frac 12 \cdot \frac{4u}{u^2 + 1} \cdot 2u = \frac {4u^2}{u^2+1}$$und die soll nun 3,6 Flächeneinheiten groß sein - also$$\begin{aligned} A_{ORQ} &= 3,6 \\ \frac {4u^2}{u^2+1} &= 3,6 \\ 4u^2 &= 3,6u^2 + 3,6 \\ 0,4u^2 &= 3,6 \\ u^2&=9 \\ u &= \pm 3 \end{aligned}$$Der Wert \(u=-3\) ist genauso eine Lösung. Das Dreieck befindet sich dann auf der anderen Seite von \(O\).

Gruß Werner

Comments

ja, ich habe es danach selber herausgefunden. Aber danke trotzdem!