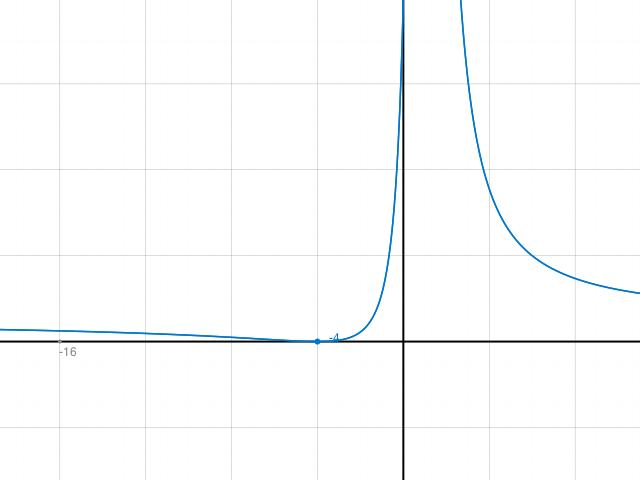
Die Skizze zu a)
B = [-4,?0?) Gemäss Abb. Vielleicht. Rechnung unten zeigt etwas anderes!
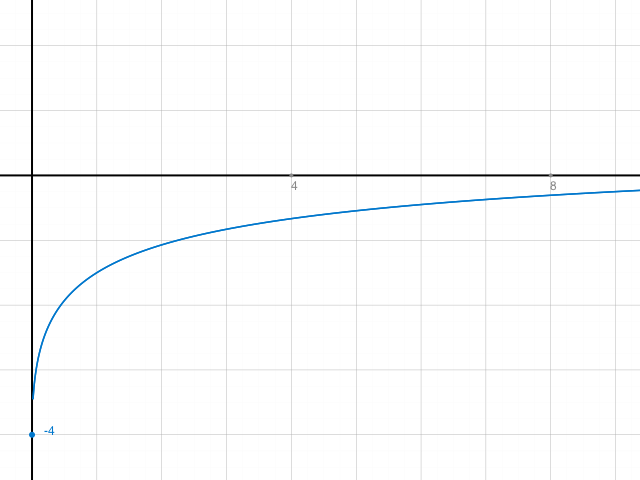
y=\frac { \sqrt { x } -4 }{ \sqrt { x } +1 } =\frac { \sqrt { x } +1\quad -5 }{ \sqrt { x } +1 } \quad =\quad 1\quad -\frac { 5 }{ \sqrt { x } +1 } \\ \\ \\ \\ Ω
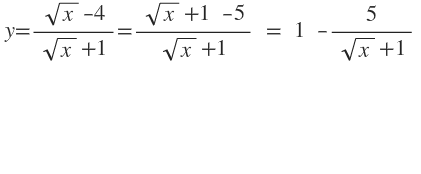
Also B= [-4, 1). -4 wird erreicht bei x=0. 1 ist der Grenzwert für x gegen unendlich.
√x ist immer > 0. → keine Definitionslücken für x>0.
Die Funktion ist monoton steigend, da der 2. Term der Subtraktion monoton fällt.
Daher ist die Umkehrbarkeit gegeben. f^{-1} (x) ist berechenbar.
Funktionsgleichung folgt.
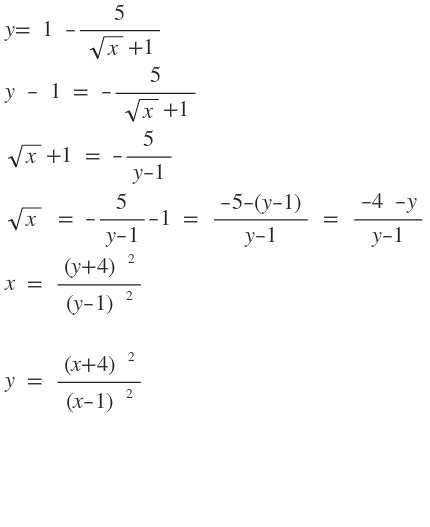
y=\quad 1\quad -\frac { 5 }{ \sqrt { x } +1 } \\ y\quad -\quad 1\quad =\quad -\frac { 5 }{ \sqrt { x } +1 } \\ \sqrt { x } +1\quad =\quad -\frac { 5 }{ y-1 } \\ \sqrt { x } \quad =\quad -\frac { 5 }{ y-1 } -1\quad =\quad \frac { -5-(y-1) }{ y-1 } \quad =\quad \frac { -4\quad -y }{ y-1 } \\ x\quad =\quad \frac { (y+4){ \quad }^{ 2 } }{ (y-1){ \quad }^{ 2 } } \\ \\ y\quad =\quad \frac { (x+4){ \quad }^{ 2 } }{ (x-1){ \quad }^{ 2 } } \\ \\ \\ \\
Am Graph der Umkehrfunktion sieht man gut, dass diese im Def. Bereich [-4,1) das Spiegelbild der ursprünglichen Funktion ist.: