Konstruieren von Strecken

Question

Aufgabe:

Gegeben sind zwei nicht parallele Geraden g und h, deren Schnittpunkt S außerhalb des
Zeichenblatts liegt und ein Punkt P.
Konstruieren Sie Strecke PS.

Beachten Sie, dass verschiedene Orte für den Punkt P möglich sind.
Es reicht nicht, die Spezialfälle P ∈ g oder P ∈ h zu betrachten.

Problem/Ansatz:

Die Spezialfälle leuchten mir ein, jedoch habe ich keine Ahnung wie ich die anderen Fälle konstruieren soll.

Comments

Konstruiere

- den Lotfußpunkt A von P auf g
und den Lotfußpunkt B von P auf h

- die Parallele g' zu g durch P
und die Parallele h' zu h durch P

- den Schnittpunkt A' des Kreises um P durch A mit h'
und den Schnittpunkt B' des Kreises um P durch B mit g'

- das Parallelogramm PB'P'A'

Die Gerade PP' ist die gesuchte Gerade PS.

---

Nachtrag : Im dritten Schritt gibt es evtl. jeweils mehr als einen Schnittpunkt.
Je nach Lage von P in den vier durch g und h definierten Quadranten sind die richtigen zu wählen.

---

Hallo

Die Strecke PS passt ja nicht unbedingt auf das Papier?

die Gerade PS konstruiert man mit Desargue, mit Strahlensatz kann man dann die Länge von PS bestimmen und falls passt zeichnen

lul

Answer 1

Hallo,

die Grundidee für folgende Konstruktion besteht darin, das Parallelogramm welches sich aus den Geraden \(g\) und \(h\) und dem Punkt \(P\) ergibt, als ähnliches Parallelogramm noch einmal zu konstruieren

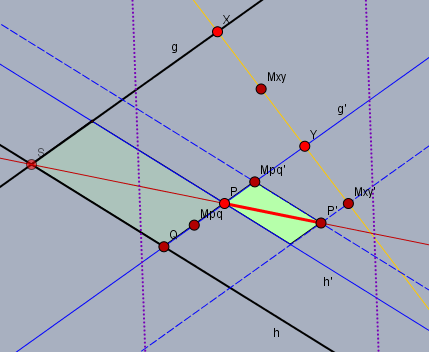
Oben im Bild sollen die gepunkteten lila Geraden die Grenzen des Zeichenblattes darstellen.

Dazu zeichnet man durch den Punkt \(P\) die Parallelen \(g'\) und \(h'\) (blau) zu \(g\) und \(h\) (schwarz). Anschließend konstruiert man ein zweites Geradenpaar (blau gestrichelt), mit Geraden die ebenfalls parallel zu \(g\) und \(h\) verlaufen. Dabei muss lediglich das Verhältnis der Abstände zu dem ursprünglichen Geradenpaar eingehalten werden.

ich bin oben in der Skizze davon ausgegangen, dass für einen ganzen Abstand kein Platz auf dem Zeichenblatt ist. Daher habe ich die Abstände des ursprünglichen Geradenpaares halbiert. Dies lässt sich immer realisieren indem man eine beliebige Gerade \(XY\) (gelb) zeichnet und die Strecke zwischen den Schnittpunkten mit \(g\) und \(g'\) halbiert. Den Mittelpunkt \(M_{xy}\) habe ich dann an \(Y\) gespiegelt und durch den neuen Punkt \(M_{xy}'\) zeichnet man wieder eine Gerade, die parallel zu \(g\) bzw. \(g'\) verläuft.

Das neue Geradenpaar schneidet sich in \(P'\). Die Strecke \(PP'\) (rot) ist genau halb so lang wie die gesuchte Strecke \(PS\).

Sollte \(P\) 'außerhalb' des Bereichs liegen, den \(g\) und \(h\) einschließen, ändert sich dadurch nichts.

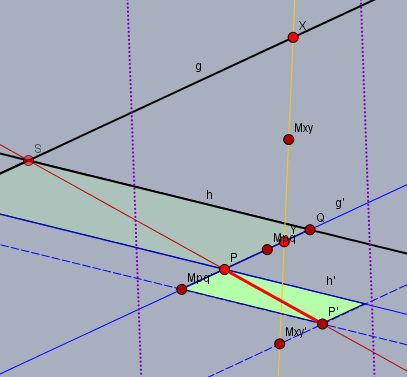
Weiter kann man statt des Faktors \(1/2\) auch jeden anderen Faktor für den Abstand des zweiten Paares wählen. Oder man zeichnet das zweite Geradenpaar gleich durch die Mittelpunkte \(M_{xy}\) und \(M_{pq}\), je nachdem wie Platz auf dem Zeichenblatt ist.

Gruß Werner