Hallo,
Bei welchen ganzen Zahlen ist das Quadrat der Zahl... um 24 größer als das Doppelte der Zahl?
Nenne die gesuchte Zahl \(x\). Das Quadrat von \(x\) ist \(x^2\). Das Doppelte von \(x\) ist \(2x\). Das Quadrat soll größer sein als das Doppelte des Zahl, und zwar um 24. Wenn man also zum Doppelten noch mal 24 hinzu addiert, dann sollte dieser Wert genau dem des Quadrats entsprechen:$$x^2 = 2x + 24$$
Stelle die Gleichung auf ...
ist damit erledigt. (s.o.)
... und löse sie zeichnerisch
jetzt wird's spanned ;-) eine Methode besteht darin, die Normalparbel zu zeichnen (das ist das \(x^2\)) und diese mit der Geraden \(2x+24\) zum Schnitt zu bringen. Die Schnittpunkte sind dann die Lösung. Das sieht so aus:
Die eine Lösung ist \(x_1=-4\) und wenn Du das in die Gleichung einsetzt kommt auf beiden Seiten \(16\) heraus. Und die zweite Lösung vom rechten Schnittpunkt ist \(x_2=6\) und wenn man dies in die Gleichung oben einsetzt, so sollte auf beiden Seiten der Wert \(36\) berechnet werden.
Finde ich persönlich aber uncool, deshalb hier noch ein zweites Verfahren.
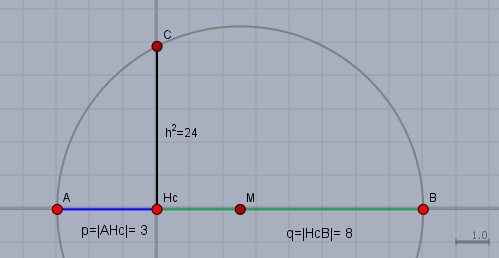
Dazu muss man wissen, dass in einem Halbkreis folgende Gesetmäßigkeit gilt: wenn man in einem Halbkreis an einer beliebigen Stelle eine Senkrechte auf den Durchmesser einzeichnet, dann ist das Produkt der beiden Streckenabschnitte auf dem Durchmesser gleich dem Quadrat des Abschnitts der auf der Senkrechten durch den Halbkreis begrenzt wird.
Oben auf dem Bild nenne ich die Strecke \(|CH_c|=h\) (schwarz) und die Streckenabschnitte \(|AH_c|=p\) (blau) und \(|H_cB|=q\) (grün). Dann gilt immer $$p \cdot q = h^2$$Das nennt man den 'Höhensatz' - vielleicht hast Du schon davon gehört. Damit man das verwenden kann, muss ich die quadratische Gleichung von oben noch ein wenig umstellen:$$\begin{aligned}x^2 &=2x + 24 &&|\,-2x \\x^2 -2x &= 24\\ \underbrace{x}_{=p}\cdot \underbrace{(x-2)}_{=q}&=\underbrace{24}_{=h^2}\end{aligned}$$Wir beginnen damit die Höhe \(h\) zu konstruieren. Dazu benötigt man ein Produkt, das 24 ergibt. Man könnte auch \(1 \cdot 24 =24\) wählen - sowas ging immer - aber es zeichnet sich gefälliger, wenn die Größenordnung beider Zahlen nicht zu sehr aus einander liegt.
Ich habe oben \(3 \cdot 8 = 24\) gewählt. D.h. man zeichnet die beiden Streckenabschnitte \(p=3\) (blau) und \(q=8\) (grün) und über den Mittelpunkt \(M\) der gemeinsamen Strecke \(p+q\) zeichnet man einen Halbkreis. Die Senkrechte in \(H_c\) am Berührpunkt der beiden Abschitte schneidet den Halbkreis dann in \(C\). Damit ist unser \(h=|H_cC|\) mit \(h^2=24\) fertig (s. Bild oben).
Jetzt weiß man zwar nicht wie lang das \(x\) alias \(p\) ist, aber wir wissen, dass \(q\) um \(2\) länger als \(p\) sein muss.
Und diese Strecke der Länge 2 zeichne ich nun als rote Strecke \(XH_c\) ein.
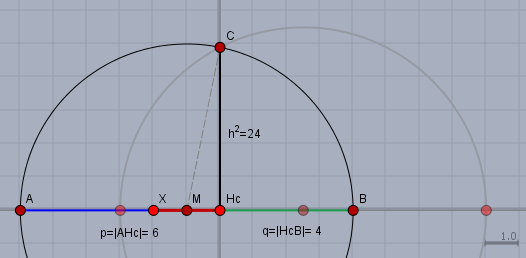
Die Strecke von \(X\) nach \(A\) (blau) muss nun genau so lang sein, wie die von \(H_c\) nach \(B\) (grün). Folglich liegt der Mittelpunkt \(M\) des neuen Kreises genau in der Mitte der roten Strecke \(XH_c\). Und der Radius \(r\) des Kreises ist zwangsläufig \(r=|MC|\). Also schlägt man einen Kreis um \(M\) mit Radius \(|MC|\), der die Waagerechte in \(A\) und \(B\) schneidet.
Und die Lösung lässt sich nun aus der Zeichnung abmessen$$(p,\,q) = (x,\,x-2) = (|AH_c|=6,\, |H_cB|=4) \implies x=6$$Und da beide Zahlen auch negativ sein dürfen (ihr Produkt ist wieder positiv) gibt es noch eine zweite Lösung$$(p,\,q) = (x,\,x-2) = (-4,\, -6) \implies x=-4$$hier mauss man nur beachten, dass \(-6\) die kleinere Zahl von beiden ist, und damit die Rolle von \(q=x-2=-6\) übernimmt.
Diese zweite zeichnerische Lösung hat den Vorteil, dass man sie mit einem Lineal (mit Maßeinteilung) und einem Zirkel erstellen kann. Eine Parabel lässt sich damit nicht so einfach zeichnen.
Gruß Werner