Bestimme den Parameter k so, dass das Integral den angegebenen Wert hat.

Question

Aufgabe:

Bestimme den Parameter k so, dass das Integral den angegebenen Wert hat.

\( \int\limits_{0}^{1} \) (e^x-k)dx=0

Problem/Ansatz:

Ich weiß leider nicht wie ich hier vorgehen soll, ich hoffe jemand kann mir weiter helfen.

Answer 1

Du fängst an, indem du das bestimmte Integral einfach mal ausrechnest. Aus k wird dabei k*x, die e-Funktion ändert sich beim Integrieren nicht. Hinterher hast Du eine Gleichung, die Du nach k auflöst.

Answer 2

Rechne einfach das Integral aus, gibt e^(-1) - k .

Also muss k= e^(-1) sein.

Comments

"Also muss k= e^(-1) sein."

Meinst du das wirklich so?

Answer 3

"Bestimme den Parameter k so, dass das Integral den angegebenen Wert hat.\( \int\limits_{0}^{1} \) (\( e^{x} \) - k )*dx=0"

\( 0=\int \limits_{0}^{1}\left(e^{x}-k\right) \cdot d x=\left[e^{x}-k \cdot x\right]_{0}^{1}=\left[e^{1}-k\right]-\left[e^{0}\right]=e-k-1 \)
\( e-k-1=0 \)
\( k=e-1 \)

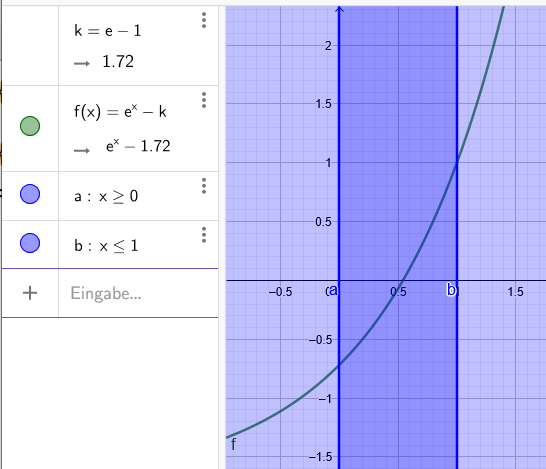
Text erkannt:

\begin{tabular}{|l|l|l|l|l|}
\hline \( \mathrm{k}=\mathrm{e}-1 \) & \( \vdots \) & 2 \\
\hline & \( \rightarrow 1.72 \) \\
& \( \mathrm{f}(\mathrm{x})=\mathrm{e}^{\mathrm{x}}-\mathrm{k} \) \\
& \( \rightarrow \mathrm{e}^{\mathrm{x}}-1.72 \) \\
& \( \mathrm{a}: \mathrm{x} \geq 0 \) \\
& \( \mathrm{~b}: \mathrm{x} \leq 1 \)
\end{tabular}