ich habe ein Verständnis Problem mit dem Integralsatz von Gauß.
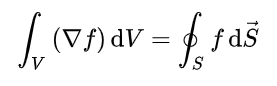
Es geht um die Herleitung der Finite Volumen Methode bei inkompressibler Navier Stokes Gleichung.
Ich verstehe hier nicht, wieso auf den Teil des Integranden wo der Gradient des kinematischen Drucks steht, auch der Satz von Gauß angewandt wird. Ich dachte man braucht hier einen Ausdruck mit Divergenz.
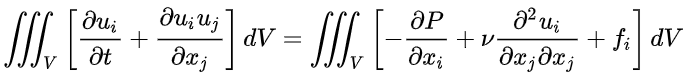
Text erkannt:
\( \iiint_{V}\left[\frac{\partial u_{i}}{\partial t}+\frac{\partial u_{i} u_{j}}{\partial x_{j}}\right] d V=\iiint_{V}\left[-\frac{\partial P}{\partial x_{i}}+\nu \frac{\partial^{2} u_{i}}{\partial x_{j} \partial x_{j}}+f_{i}\right] d V \)
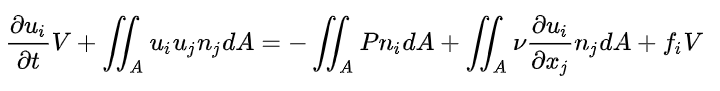
Text erkannt:
\( \frac{\partial u_{i}}{\partial t} V+\iint_{A} u_{i} u_{j} n_{j} d A=-\iint_{A} P n_{i} d A+\iint_{A} \nu \frac{\partial u_{i}}{\partial x_{j}} n_{j} d A+f_{i} V \)
Ps: Bin neu hier und hab die Formeln in Word getippt und dann per Screenshot eingefügt. Hoffe das ist ok.
