Konstruktion am Dreieck

Question

Aufgabe:

Konstruiere ein Dreieck $\mathrm{ABC}$ aus $\mathrm{c}=5 \mathrm{~cm} ; \mathrm{b}=3,5 \mathrm{~cm} ; \mathrm{a}=2,7 \mathrm{~cm}$.

a) Von welchen Punkten aus sieht man die Seite $\overline{\mathrm{AC}}$ unter einem Winkel von $40^{\circ}$ und die Seite $\overline{\mathrm{AB}}$ unter einem Winkel von $30^{\circ}$ ?

b) Gibt es einen Punkt, von dem aus man alle drei Seiten unter demselben Winkel sieht?

Problem/Ansatz:

Ich möchte GERN zuesrt den Sachverhalt ( Tel a ) versethen.

Ich habe den Sachverhalt ( Teil a)  NICHT verstaden , obwohl ich JESED WORTE verstehe und habe MEHRS MALS gelesen.

Bedeutet Teil a) --->Dieser Satzt: Von welchen Punkten aus sieht man die Seite AC unter einem Winkel von 40 und Ab von30?

was ist richtg ( mein Satz no1 oder 2)
Bedeutet ,dass es gibt viele Punkte und aus diesen vielen Punkten

1)gibt es NUR einen Punkt aus dem sieht amn AC unter 40 und AB unter 30 (Gleichzeitig)

oder

2) gibt es einen Punkt aus dem sieht man AC unter 40 und NOCH EINEN ANDREN aus dem sieht man AB unter 30 sieht

hier ist meine Zeichnung.

Comments

was ist richtg ( mein Satz no1 oder 2)

Keiner ist ganz richtig.

Satz 2 ist falsch. Die Beobachtung der beiden Strecken AB und AC findet gleichzeitig statt.

Satz 1 (gibt es NUR einen Punkt) ist hier aber auch nicht richtig, weil es bei diesen speziellen Maßen des Dreiecks mehrere geeignete Punkte gibt.

Answer 1

Hallo Zahri,

betrachte zunächst nur die Seite $AC=b$ des Dreiecks. Ich habe die Seite unten dick blau markiert.

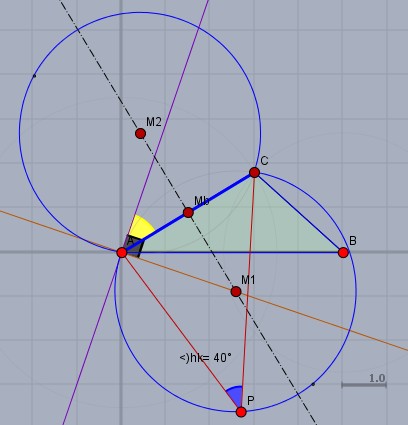
Wenn Du die Seite $AC$ von einem beliebigen Punkt $P$ aus unter einem Winkel (blau) von $40°$ siehst, so befindet sich dieser Punkt auf einem der blauen Kreisbögen. Diese Bögen nennt man Fasskreisbögen.

Zur Konstruktion legst Du den gewünschten Winkel von $40°$ (gelb) an die Strecke $AC$ in dem Punkt $A$ oder $C$ an. Welcher von beiden ist egal. Das ist der gelbe Winkel oben im Bild mit dem lila Schenkel. Dann konstruiert man im gleichen Punkt (hier $A$) eine Senkrechte (braun) auf dem Schenkel des Winkels. Diese Senkrechte schneidet dann die Mittelsenkrechte (schwarz) der Strecke $AC$ im Mittelpunkt $M_1$ des Fasskreisbogens.

Da es immer zwei solcher Bögen gibt, kannst Du $M_1$ noch an der Seite $AC$ spiegeln und bekommst $M_2$. Die Kreise um $M_1$ bzw. $M_2$ mit dem Radius $|M_1A|$ bilden dann die gesuchten Bögen.

Machst Du das gleiche für die Strecke $AB$ und dem Winkel $30°$ (grün), ....

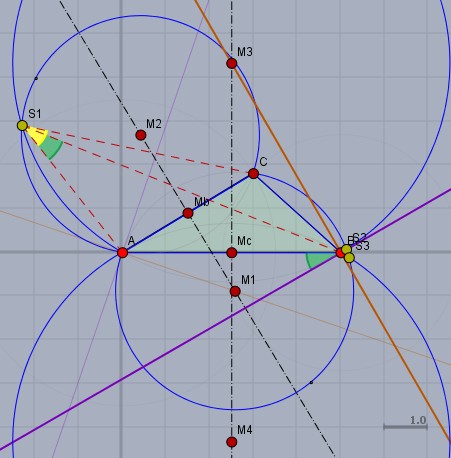
.... so erhältst Du zwei weitere Fasskreisbögen mit den Mittelpunkten $M_3$ und $M_4$ (s. Bild). Und es existieren in Summe drei Schnittpunkte $S_1$, $S_2$ und $S_3$ mit dem anderen Bogenpaar.

Bei $S_1$ habe ich die beiden Winkel von $40°$ (gelb) und $30°$ (grün) eingezeichnet. Die Punkte $S_2$ und $S_3$ liegen ganz dicht beim Punkt $B$. Von jedem der drei Punkte sieht man die Strecke $AC$ unter $40°$ und die Strecke $AB$ unter $30°$.

Gruß Werner

Comments

@WS : Interessant ist die Sonderstellung von S2 im Vergleich mit S1 oder S3 (spielt für die Beantwortung der Frage b) eine Rolle)

---

(spielt für die Beantwortung der Frage b) eine Rolle)

Du meinst den Fermat-Punkt - oder?

---

Natürlich wird in Aufgabe b) dieser Fermat-Punkt gesucht.

Meine Überlegungen gingen in folgende Richtung :
Von Punkt S1 aus sehe ich mit dem rechten Auge Punkt A und mit dem linken Auge wahlweise Punkt B (30°) oder Punkt C (40°).
Von Punkt S3 aus sehe ich mit dem linken Auge Punkt A und mit dem rechten Auge wahlweise Punkt B (30°) oder Punkt C (40°).
Wenn ich aber von Punkt S2 aus mit z.B. dem rechten Auge A fixiere, dann sehe ich mit dem linken Auge zwar B unter einem Winkel von 30°, C aber unter einem Winkel von 320°. Man muss "den Kopf drehen" , so dass A mit dem anderen Auge gesehen wird, um auf 40° zu kommen. Und ich denke, dass die Aufgabe trotzdem von einem Sehwinkel von 40° und nicht 320° ausgeht, damit b) mit "ja" beantwortet werden kann.

PS. : Die Überschrift wird immer blöder.

Answer 2

Der Punkt P ist derjenige, von dem aus du AC unter 40° und AB unter 30° siehst:

Comments

ich möchte SEHR GERN , die Zeichnung wie ich oben gemacht habe ( Richtung ABC) weiter maachen. Also wenn ich richtig dich verstehe. du meinst es gibt EINEN PUNKt( P) und aus diesem Punkt sehe ich GLEICHZEITÍG AC unter 40 und AB unter 30 und NICHT einen Punkt für AC und einen ANDREN punkt ( Beispiel T) für AB. stimmt? wenn ja.

mein sehr sehr wichtig Frage: wie bist du dazu gekommen, das ist SO gemeint und NICHT

einen Punkt P für AC und eine ANDREN Punkt T für AB? diese frage ist mir UNGLAUBLICH wichtig , denn ich habe Schwierigkeiten den TEXT ZU VERSTEHEN: dann machen wir weiter.

so

---

Ich habe deine Skizze als Grundlage benutzt:

Die wichtigste Frage ist jetzt: Wie konstruiert man den Punkt P?

Deine sehr sehr wichtige Frage: wie bist du dazu gekommen, das ist SO gemeint und NICHT einen Punkt P für AC und eine ANDREN Punkt T für AB?

Können wir nicht gleichzeitig besprechen. Diese Frage hat etwas mit deinem Verstehen deutscher Sprechweisen zu tun. Das lenkt aber von dem mathematischen Inhalt der Aufgabe zu sehr ab.

---

Zitat "Können wir nicht gleichzeitig besprechen. Diese Frage hat etwas mit deinem Verstehen deutscher Sprechweisen zu tun. Das lenkt aber von dem mathematischen Inhalt der Aufgabe zu sehr ab." '

meinst du ich habe die Aufgabe nicht verstanden, wegen der Sprache der Mathe Hintergrund?

ich verstehe aber JEDES WORT sprachlich. Also warum habe nicht den Text nicht verstanden. MIr wurde bestätigt. KOGNITIVE DEFIZITE, nach neurologischen Bereich. Aber Intelligenz ,sagt er NORMAL: was bedeutet das? Warum kann ich den Text OFT versthen. Was sloo ich machen. ? ich habe soviel Logopädie und Ergotherapie ,sehe aber KEINE deutliche Besserung. ich habe bae ruch manchmal beim Arabisch so. Ich denke das hat NICHT zu tun mit sprach, oder?

---

@Zahri: Ich finde es sehr gut, dass du jedes Wort der deutschen Sprache verstehst und ich beglückwünsche dich dazu.

Leider ist das Buch, welches ihr benutzt, sehr schlecht. In diesem Falle ist der Text der Aufgabe

"a) Von welchen Punkten aus sieht man die Seite $\overline{\mathrm{AC}}$ unter einem Winkel von $40^{\circ}$ und die Seite $\overline{\mathrm{AB}}$ unter einem Winkel von $30^{\circ}$ ?"

sehr leicht falsch zu verstehen.

In demselben Buch müssen vorher andere Aufgaben gestanden haben, wie zum Beispiel:

"Konstruere eine Strecke $\overline{AB}$ und die Menge aller Punkte, von denen aus die Strecke $\overline{AB}$ unter einem Winkel von 40° erscheint."

Die Aufgabe a) muss in diesem Zusammenhang verstanden werden.

---

ich möchte NUR wissen erstmal WO IST DER SCHÜLLESWORT, dass ich so verstehe ,das es NUR einen Punkte ,aus dem ich AB und AC , und NIHCT 2 oder drei Punkt? Wo ist dem Schlüsselwort? Dann mache weiter. mit der Lösung.

---

@Zahri: Dein Buch ist hier sehr schwer zu verstehen. Das ist nicht deine Schuld und hat auch nichts mit deinen Sprachkenntnissen zu tun. Das ist ein Mangel des Buches.

Das SCHLÜSSELWORT markiere ich rot:

Von welchen Punkten aus sieht man die Seite $\overline{\mathrm{AC}}$ unter einem Winkel von $40^{\circ}$ und die Seite $\overline{\mathrm{AB}}$ unter einem Winkel von $30^{\circ}$ ?

Das kann man auch so verstehen, wie du es verstanden hast: "Für jede Strecke gibt es einen anderen Punkt."

---

Das kann man auch so verstehen

Wenn man es aber so versteht, dann macht man einen Fehler.

Dein Schlüsselwort ist Unfug, siehe meinen ersten Kommentar und WSs Lösung. Es geht nicht um den Plural, das Schlüsselwort ist "und" !

"Welche natürlichen Zahlen unter 20 sind durch 2 und durch 3 teilbar ?" hat ganz eindeutig nur die Lösungen 6 , 12 , 18, aber nicht etwa wie du suggerieren möchtest eventuell auch noch 4, 8, 9, 10, 14, 15, 16

---

ok wir werden weiter machen ,aber NUR kürze Frage zu Gasthi2016

also meinst du --->1)gibt es MEHRERE Punkte ( Beispiel ( T, K ,M)  und ich kann bei JEDEM PUNKT ( Beipiel T)den AC unter 40 und gleichzeitig AB unter 30  sehen?.

und wenn ich noch den Punk (k)nehme dann ich AUCH    AC unter 40 und gleichzeitig AB unter 30 . sehen.?

und wenn ich Punkt (M) nehme dann kann ich AUCH    AC unter 40 und gleichzeitig AB unter 30 . sehen.?
so meinst du?

---

also meinst du --->1)gibt es MEHRERE Punkte ( Beispiel ( T, K ,M)  und ich kann bei JEDEM PUNKT ( Beipiel T)den AC unter 40 und gleichzeitig AB unter 30  sehen?.

Ja - es gibt drei Punkte. Ich habe diese drei Punkte in meiner Antwort mit $S_1$, $S_2$ und $S_3$ bezeichnet. Von jedem(!) dieser drei Punkte aus sieht man gleichzeitig $AC$ unter $40°$ und $AB$ unter $30°$.

Ich habe diese drei Punkte gelb markiert (s. zweites Bild in meiner Antwort).

---

zuesrt : ist das eine logische Frage: warum wenn ich untn eine 40 Grad Winkel eintrage ,( blau) dann bekomme ich OBEN ein 50 Grad winkel( rot) . Also oben fasskreiswinkel 50 und unten Jazzkreiswinkel 40, oder diese ist UNSINNIGE Frage( maht keine SInn)

und hier

---

Hallo Zahri,

Ja - das ist richtig. Man trägt den Winkel immer auf der gegenüberliegenden Seite der Strecke ab.

Das gilt auch dann, wenn der Winkel größer ist als 90°

... (Konstruktions-)Winkel und Fasskreisbogen liegen immer auf der jeweils anderen Seite der Strecke $AB$.

---

für mich ist einfacher wenn ich erstmal NUR einen Punkt auf meine Ziehung mache?

ich versuche die Schritte zu beschrieben, du kannst aber die Schritte auch nach der Reihenfolge schrieben( 1,2, 3,)

---

HIer

HierWinkel dabei( 30 und 40 )

stimmt bis hier ? wenn  ja# möchte wissen wie komme ich zuerst zu einem ( erstmal eine Punkt)

wo ich AC unter 40 und AB unter 30 gleichzeitig sehen kann?

so ist für mich einfacher zu verstehen

also Ergänzung wäre gut

---

1. Konstruiere die Menge aller Punkte, von denen aus man die Strecke AB unter einem Winkel von 30° sieht. (Das ist ein Kreis K₁ auf dem A und B liegen)

2. Konstruiere die Menge aller Punkte, von denen aus man die Strecke AC unter einem Winkel von 40° sieht. (Das ist ein Kreis K₂ auf dem A und C liegen)

3. Jeder Schnittpunkt von K₁ und K₂ ist ein Punkt, von dem aus man die Seite $\overline{\mathrm{AC}}$ unter einem Winkel von $40^{\circ}$ und die Seite $\overline{\mathrm{AB}}$ unter einem Winkel von $30^{\circ}$ sieht.

---

Hallo Zahri,

ich habe die Konstruktion bereits in meiner Antwort beschrieben. Du solltest ganz konkrete Fragen stellen, wenn Du etwas nicht verstehst.

Aber ok, anbei nochmal für diesen einen Punkt:

1.) Zeichne die Mittelsenkrechte der Strecke $AC$ (schwarze Strich-Punkt-Gerade durch $M_b$)

2.) Trage den Winkel 40° unterhalb der Seite $AC$ im Punkt $C$ an (gelb). Der Schenkel ist lila gezeichnet.

3.) errichte im Punkt $C$ die Senkrechte (braun) auf dem Schenkel.

4.) Die Senkrechte (braun) schneidet die Mittelsenkrechte (schwarz) im Punkt $M_2$

5.) Zeichne den Fasskreisbogen oberhalb der Strecke $AC$ mit Mittelpunkt $M_2$ und Radius $|M_2A|$.

wiederhole die Schritte 1 bis 5 für die Strecke $AB$ und den Winkel 30° (grün). Der zweite Fasskreisbogen über $AB$ schneidet den Bogen über $AC$ im Punkt $S_1$ (gelb).

Vom Punkt $S_1$ sieht man gleichzeitig die Strecke $AC$ unter 40° und die Strecke $AB$ unter 30°.

---

... möchte wissen wie komme ich zuerst zu einem ( erstmal eine Punkt)
wo ich AC unter 40 und AB unter 30 gleichzeitig sehen kann?

:-)) da wo sich die beiden Kreise schneiden!

Von jedem Punkt des 40°-Fasskreisebogens siehst Du die Strecke $AC$ unter 40° und von jedem Punkt des 30°-Fasskreisbogens sieht man die Strecke $AB$ unter 30°.

Daraus folgt (ganz logisch!) dass von dem Punkt aus, in dem sich die beiden Bögen schneiden, Du sowohl die Strecke $AC$ unter 40° als auch gleichzeitig die Strecke $AB$ unter 30° siehst!

---

HAbe ich richtig gemacht? Ich habe die Winkel von Unten geändert. früher aheb dien 30 und 40 bei ( A) getragen

jetzt NUR 40 bei ( A) und (30) habe ich bei C, deswqegn kommen BEIDE Kreis im obenigen Bereich, vorher war ein Kreis oben und andere Unten, jetzt BEIDE oben. stimmt so?

---

So stimmt es. ..............

---

gut wir machen morgen weiter. Jetzt nur frage

WOher soll ich wissen ,dass ich die Ecke ( A)  mit (30 Grad) oben

,

zu Ecke ( C) unten ( 30) wechseln soll? ich habe das ZUFALL gemacht.

snsot kann noch die Aufagbe lösen oder?

---

Woher soll ich wissen ,dass ich die Ecke ( A)  mit (30 Grad) oben ... zu Ecke ( C) unten ( 30) wechseln soll?

Das musst Du nicht wissen. Zu jeder Strecke gehört ein Paar Fasskreisbögen. Und es sind alle Schnittpunkte des einen Bogenpaares mit dem anderen Bogenpaar gesucht. In Deinem Fall gibt es drei solcher Schnittpunkte.

---

ic habe früher umgekehrt gemacht( AB habe unter 40 und AC unter 30 ) ih habe korrigiert

stimmt so?
wenn ja

dann noch Frage

---

Ja - jetzt erst stimmt es. Hatte ich auch übersehen.

---

aha, du hast AUCH übersehen? ok

jetzt klein Tipp zur → wo sind die ander 2 Punkten,von jedem ich auch gleichzeitig AB und AC sehen kann wie ( M)? Also hast du NUR klein Tipp?

---

Ich antworte erst wieder, nachdem du das Aufgabenblatt bearbeitet hast, das ich dir per E-mail sandte.

---

wo sind die ander 2 Punkten,von jedem ich auch gleichzeitig AB und AC sehen kann wie ( M)? Also hast du NUR klein Tipp?

Das steht in meiner Antwort ... lies diese bitte durch!

Und einen der beiden anderen Punkte hast Du doch selber schon gefunden. Schau Dir Dein Bild an, wo ich den rotenPfeil eingefügt habe. Und der dritte Punkt wird von den Fasskreisbögen erzeugt, die sich unterhalb von $AB$ und $AC$ befinden.

---

ZUerst veieln Danke FÜR ALLE , weil ALLE hier sind sehr aktive, ja aber wiel du die Lösung östängig auf einmal gelöst, ist FÜR MiCH ,weil ich behindert war schwer ALLES zu merken, deswegen habe nur in Schritte geamcht. Ich gücke die Lösung morgen in Ruhe und melld mich.

---

HAllo ,

ich stelle die ZWEi Lösungen untereinander, um schnelle r zu gucken)

1) die erst Lösung( erster Punkt)

jetzte zweiter LÖsung( der Punkt ist blau, befindet sich rechts)

noch mal größer( von diesem blauen Punkt sieht man AC unter 40 und AB unter 30)

noch mal größer. stimmt so?

stimmt so?

---

stimmt so?

Ja das stimmt so und es ist erstaunlich, dass Du fragst, weil genau diesen Punkt habe ich in meiner Antwort beschrieben. Du musst doch nur Deine Ergebnisse mit meiner Antwort vergleichen.

---

ich versthe NUR sehr langsam. Ok also jetzt zwei Punkt: gib es noch dritte Punkt ? wenn ja ,dann werde erstmal allein denken, weil ich lernen möchte, Ih habe ja diene Lösung früher gehsehn, es war unglaublich für mich schwer, weil du hast die Aufgabe auf einmal gelöst, ich kann schrittweise verstehen

---

hallo,

ich m;che GERN der dritte PUnkt fndden.

HIer ist was ich gemacht habe.

Erster PUnkt (p1):

Jetzt zweiter Punkt (p2)

Text erkannt:

jetzte zweiter LÖsung( der Punkt ist blau, befindet sich rechts):

Jetzt weiss ich NIHCT mehr , wo ich der dcritte Punkt POSITIONIEREN kannn, weil der dritte Punkt( P3)muss auch an den Schnitt von diesen zwei Kreisen leigen, wie beim (P1) und (P2)?Kannst du NUR der dritte Punkt erstllen, das ist für mich VIEL leichter zu folgen und versthen als wenn ALLE Punkte auf einmal da, das ist für mich schwer. Ich brauch NUR der dritte Punkt,dannach sit die Aufgabe VOLLSTÄNDIG erledigt

---

Hallo Zahri,

der dritte Punkt liegt genau so rechts vom Punkt $B$ des Dreiecks, nur etwas höher als der zweite.

oben habe ich den Punkt gelb markiert.

Es ist der Schnittpunkt des unteren Fasskreisbogens von $AC$ mit dem oberen Fasskreisbogen von $AB$.

Hier noch mal im Detail:

der blaue Winkel beträgt 40° zur Seite $AC$ und der gelbe Winkel 30° zur Seite $AB$

Gruß Werner

---

habe leider NIX verstanden.

wir nennen die Punkten S1 , S2 und S3

erste Lösung--> S1( rot), wichtig zu sagen, zwei Umkreis befinden sich beide OBEN ( lila und grün)

zweite Lösung S2( rot) wichtig zu sagen, zwei Umkreise befinden sich beide

UNTEN ( schwarz  und blau)

jwir haben jetzt SCHON zusammen 4 Kreis für S1 und S2.

jetzt wenn ich den dritten Punkt S3 bestimmten würde, muss ich ZUSÄTZLICH NOCH ZWIE KRIES ZEICHEN , wie bei S1 Und bei S2 oder nicht? weil S3 muss auch auf den Schnittepuknt zweier Kreis leigen. oder? wie beim S1 und S2.

---

habe leider NIX verstanden.

Ok ... was genau hast Du an folgendem Satz aus meinem Kommentar oben nicht verstanden?

ich schrieb:

Es (der dritte Punkt) ist der Schnittpunkt des unteren Fasskreisbogens von $AC$ mit dem oberen Fasskreisbogen von $AB$.

jetzt wenn ich den dritten Punkt S3 bestimmten würde, muss ich ZUSÄTZLICH NOCH ZWIE KRIES ZEICHEN , wie bei S1 Und bei S2 oder nicht?

Nein das ist nicht nötig. Du nimmst zwei Kreise bzw. zwei Fasskreisbögen, die schon da sind!

1. Fasskreisbogen über der Seite $AB$ OBEN (lila)

2. Fasskreisbogen über der Seite $AC$ UNTEN (blau)

diese beiden Fassbögen schneiden sich in $S_3$ (oben im Bild gelb markiert.)

---

ich wa r beim Arzt, ich lese und melde mich später

---

Hallo m Werner,

stimmt so?

ich hab noch mal gemacht( habe Winkle gelöscht) um besser zu sehen

noch mal größer

stimmt?

S2 und S3

---

Hallo Zahri,

Ja prima - ist alles richtig!

---

sehr gut. Lust auf diese Aufgabe? wäre sehr schön diese zu lösen

Jetzt Lösung im Buch

Mein Versuch

ja stimm wenn a+b>e ist dann eindeutig zwei Lösungen

a=3

b=3

e=4

aber wenn a+b=e--> wie gibt es NUR eine Lösung?

a=3

b=2

e=5

dann entsteht bi c3 einen Punkt aber wir alles zu einer LInie , ich sehe kein Dreieck meh

M

dann entsteht bi c3 einen Punkt aber wir alles zu einer LInie , ich sehe kein Dreieck mehr

Lösung

---

In welchem Zusammenhang wurd die Aufgabe gestellt:

Geht es um ein Parallelogramm?

---

ich lerne das Kapital --< Konstruktion von Vierecken. und dazu gibt es Aufgabe

Aufgabe no22  ( rot markiert)mache gerade

und hier ist die Lösung im Buch

Text erkannt:

22. Da mit e die eine Diagonale fest liegt, ist die Lösung eindeutig, wenn $a+b \leq e$ und $c+d \leq e$. Anderenfalls gibt es keine Lösung.

hier ist meine Versuch( wann eine Lösung,wann 2 Lösung wann keine Lösung)

Mein Versuch

ja stimm wenn a+b>e ist dann eindeutig zwei Lösungen

a=3

b=3

e=4

aber wenn a+b=e--> wie gibt es NUR eine Lösung?

a=3

b=2

e=5

dann entsteht bi c3 einen Punkt aber wir alles zu einer Linie , ich sehe kein Dreieck mehr





Lösung

---

Hallo Zahri,

In der Lösung ist ein Fehler. Es muss heißen:

... ist die Lösung eindeutig, wenn $a+b {\color{red}\ge} e$ und $c+d{\color{red}\ge} e$. Anderfalls gibt es keine Lösung.

zu Deiner Skizze: wenn $a=3$ und $b=2$, dann ist $a+b=5$ und wenn $e=4$ ist, so ist $5 \gt 4$ - also $a+b \gt e$. Somit kann man das Dreieck aus $a$, $b$ und $e$ konstruieren.

Die Eindeutigkeit der Lösung setzt voraus, dass das Viereck konvex sein soll, d.h. keine Innenwinkel von $\gt 180°$ vorkommen.

ja stimm wenn a+b>e ist dann eindeutig zwei Lösungen

Nein, unter den genannten Voraussetzungen gibt es nur eine Lösung. Wie sollten auch die zwei Lösungen aussehen?

@Zahri: diese Frage hat mit den Fasskreisbögen nichts zu tun. Mache bitte dafür eine neue Frage in der Mathelounge auf.

Gruß Werner

---

soll ich diese Aufgabe neu stellen_

---

soll ich diese Aufgabe neu stellen_

Wenn Dir meine Antwort genügt, so brauchst Du die Frage auch nicht nochmal einstellen.

Solltest Du noch weitere Fragen zu dem Thema (bzw. Aufgabe 22) haben, so schreibe sie bitte als Kommentar unter Deine schon gestellte Frage.

siehe https://www.mathelounge.de/917131

---

Hier habe noch öffne Frag Werner

möchte die Aufgane bis Ende erlidige bleibt kleine Frage -->

Da war meine Frage

Text erkannt:

wenn ja dann habe kürze Frag.
das, was Du auf dem Bild skizzierst hast, ist alles richtig!
Wenn Du sonst noch eine Frage hast, so versuche diese bitte in einem einzigen Satz zu formulieren und mache ein '?' an das Satzende ;-)
Kommentiert vor 3 Tagen von Werner-Salomon
Melden
Warum im kleinen Kreis kommt 90 oben oder beim größeren ( rechts) kommt der Winkel 90 UNTEN und nicht oben wie beim kleineren Kreis?

Hier der Link; möchte gern versthen

https://www.mathelounge.de/916451/der-schatten-der-kugel