Hallo,
ich nehme an, dies ist der Aufgabentext:
berechnen Sie das zweidimensionale Integral \( \int\limits_{A}^{} \) y dA
Dann ist Dein Ansatz
Also mein Ansatz \( \int\limits_{0}^{2} \) \( \int\limits_{0}^{1} \) xy dx dy ...
schon falsch, denn die Funktion \(f\) über der xy-Ebene ist lt. Aufgabe \(f(x,y)=y\) und nicht \(f(x,y)=xy\).
aber irgendwie stört mich der Normalbereichsbegriff.Damit kann ich nichts anfangen,weil ich davon nichts gehört habe.
ich auch nicht. Jedoch stellt sich bei den mehrdimensionalen Integrationen immer die Frage über welche Richtung die Hauptintegrationsrichtung läuft.
Ich interpretiere 'x-Normalbereich' mal so, dass es heißt:$$\int\limits_A y \,\text dA =\int\limits_x\int\limits_y y\,\text dy\,\text dx$$und entsprechend 'y-Normalbereich' als$$\int\limits_A y \,\text dA =\int\limits_y\int\limits_x y\,\text dx\,\text dy$$Dazu schau Dir mal dieses Bild an:
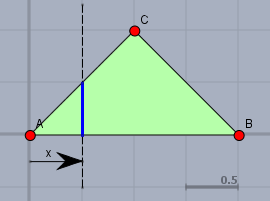
Wenn die Hauptrichtung die X-Richtung ist, muss ich mir über den blauen Bereich Gedanken machen. Und es wird auch klar, dass man in diesem Fall das Integral zweiteilt, weil die Integrationsgrenzen von \(y\) sich an der Stelle \(C\) ändern.$$\int\limits_A y \,\text dA = \int\limits_{x=0}^{1}\int\limits_{y=0}^{y=x} y \,\text dy\,\text dx + \int\limits_{x=1}^2 \int\limits_{y=0}^{y=2-x}y\,\text dy\,\text dx$$
Ist die Y-Richtung die Hauptintegrationsrichtung. Dann verlaufen die Grenzen des inneren Integrals zwischen den Seiten \(AC\) bis \(BC\).
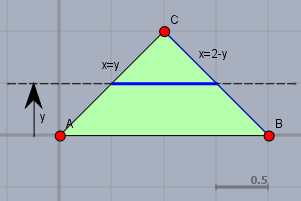
Hier kommt man mit einem Integral hin$$\int\limits_A y \,\text dA = \int\limits_{y=0}^1\int\limits_{x=y}^{x=2-y}y \,\text dx\,\text dy$$
Schau Dir das mal an. Und falls Du doch nicht zurecht kommst, so melde Dich bitte.
Gruß Werner