Hi, ich denke man kann das so machen.
Nehme \( N \) Mitarbeiter und ordne nach dem Zufallsprinzip jedem Mitarbeiter eine Zahl zwischen 1 und 365 zu. Das sollen die Geburtstage der Mitarbeiter sein. Dannn zählst Du, wieviel unterschiedliche Gebursttage es gibt.
Die Formel für die Arbeitstage hast Du ja schon selber hingeschrieben $$ \text{Anzahltage} = (365 - k) \cdot N $$
Wobei jetzt \( k \) die Anzahl der verschiedenen Geburtstage darstellt.
Du musst das Prinzip, dass ich beschrieben habe, aber mehrmals durchführen, da die Geburtstage ja immer zufällig gezogen werden. Danach bildet man den Mittelwert über alle durchgeführten Versuche und bekommt so den wahrscheinlichsten Wert an unterschiedlichen Geburtstagen, in Abhängigkeit der Mitarbeiteranzahl.
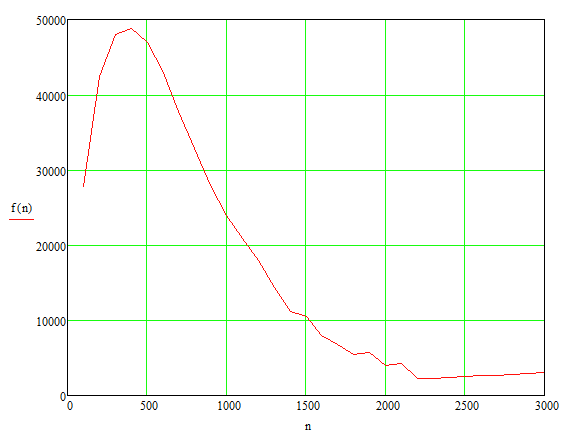
Unten eine Grafik wie es aussehen könnte. \( f(n) \) ist die Anzahl der Arbeitstage und \( n \) die Anzahl der Mitarbeiter.
Da die Berechnung lange dauert, habe ich die Anzahl der Mitarbeoter jeweils nur in hunderter Schritten berechnet und auch nur 100 Wiederholungen durchgeführt. Mir erscheint das Ergebnis plausibel, denn wenn man wenig Mitarbeiter hat, ist die Wahrscheinlichkeit gering, dass es doppelte Geburtstage gibt, aslo steigt die Anzahl der Arbeitstage am Anfang mit der Anzahl der Mitarbeiter. Bei sehr vielen Mitarbeitern steigt die Zahl der unterschiedlichen Geburtstage aber gegen 365, und damit die Anzahl Arbeitstage gegen 0.