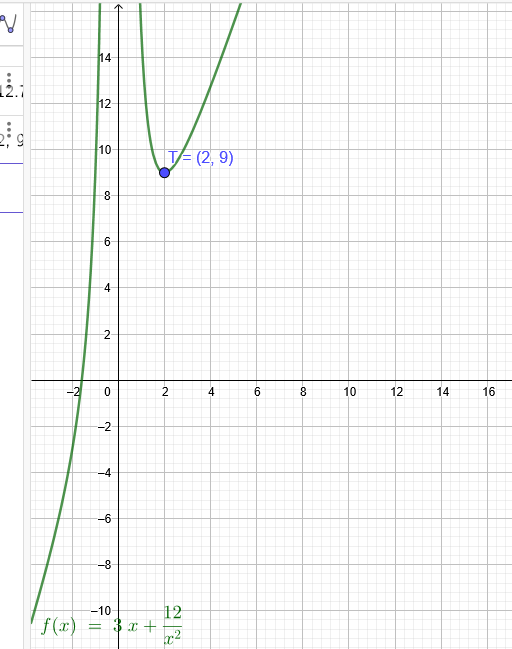
Der Graph der Funktion f mit f(x)=a*x+ \( \frac{b}{x^2} \) hat den Tiefpunkt T=(2|9).
f(2)=a*2+ \( \frac{b}{2^2} \)=2a+\( \frac{b}{4} \)
1.)2a+\( \frac{b}{4} \)=9
f´(x)=a-\( \frac{2b}{x^3} \)
f´(2)=a-\( \frac{2b}{2^3} \)=a-\( \frac{b}{4} \)
2.) a-\( \frac{b}{4} \)=0 \( \frac{b}{4} \)=a
2a+a=9 a=3 b=12
f(x)=3*x+ \( \frac{12}{x^2} \)