Abiaufgaben-Analysis: f(x)=(-x^3+5x^2-4)/(2x^2)

Question

Hallo liebe Mitglieder des Forums,

ich schreibe bald eine Klausur in Mathe und habe zur Vorbereitung Aufgaben bekommen, die ich lösen würde ,wenn ich es könnte. Ich bitte euch um eure Hilfe.

Gegeben ist die Funktion f

f(x)=(-x^3+5x^2-4)/(2x^2)

b) Die Kurve K und die drei Geraden y=-1/2x+5/2, x=1 mit t>1 begrenzen eine Fläche mit dem Inhalt A(t). Berechnen Sie A(t). Fuer welches t beträgt der Flächeninhalt 1 Flächeneinheit? Berechnen Sie lim A(t).

c) Vom Punkt S(0; -7/2) lassen sich zwei Tangenten an die Kurve K legen. S und die beiden Berührpunkte sind Eckpunkte eines Dreiecks. Berechnen Sie einen Flächeninhalt.

Meine Fragen:

zu b) Welche drei Geraden sind gemeint? Ich erkenne nur eine und zwar y=-1/2x+5/2?

      Wie gehe ich bei dieser Aufgabe vor?

zu c) Warum geht es hier um zwei Tangenten wenn nur ein Punkt vorgegeben ist?

      Wenn ich den x-Wert von S in die erste Ableitung einsetzen muss ist die Aufgabe überhaupt dann noch lösbar? oder ist meine Ableitung etwa falsch: f'(x) = -((x^3-8))/(2x^3)

      Wie berechne ich die Berührpunkte?

PS: ich möchte nochmal klar stellen,dass ich nicht von euch verlange meine Hausaufgaben zu lösen,weil ich etwa faul bin. Ich möchte verstehen wie man eine solche Aufgabe löst um später auch nicht nachfragen zu müssen.

Ich freue mich auf eure Antworten und bedanke mich schon mal im voraus!. :)

Answer 1

b) Die Kurve K und die drei Geraden y=-1/2x+5/2, x=1 mit t>1 begrenzen eine Fläche mit dem Inhalt A(t). Berechnen Sie A(t). Fuer welches t beträgt der Flächeninhalt 1 Flächeneinheit? Berechnen Sie lim A(t).

Vermutlich ist hier noch die gerade x = 1 und x = t mit t > 1 gemeint.

Comments

c)

Die Tangenten haben die Gleichungen

t1(x) = 3.5·x - 3.5

t2(x) = - 4.5·x - 3.5

Beide gehen durch S und Berühren den Graphen der Funktion.

---

Danke für die schnelle Antwort! :) Und natuerlich für die Graphik! Wie kommst du aber auf x=t? und woher wissen wir wie die Steigung von x=t ueberhaupt ist?  

---

x = t habe ich nur vermutet. das sollte in deiner aufgabe stehen. wenn dort t > 1 steht aber davor kein t gegeben ist macht das kein sinn. also entweder hast du etwas vergessen oder der lehrer.

da man aber sicher den grenzwert der fläche für t = unendlich berechnen soll. auch der grenzwert des limes fehlt in deiner aufgabe denke ich es handelt sich um die gerade x = t.

---

Achtung x = 1 und x = t sind keine Funktionen sondern senkrechte geraden im Koordinatensystem. Du findest in meiner Skizze die Gerade x = 1. Die Gerade x = t befindet sich im zweifel rechts davon.

---

Oh da hat mein Lehrer wohl was vergessen :) Vielen Dank nochmal für die super schnelle Hilfe!

---

Ich komme auf eine Fläche von

A(t) = ∫ (1 bis t) ((- 1/2·x + 5/2) - (- x^3 + 5·x^2 - 4)/(2·x^2)) dx = 2 - 2/t

Für welches t beträgt der Flächeninhalt 1 Flächeneinheit?

2 - 2/t = 1 → t = 2

Berechnen Sie lim A(t).

lim (t → ∞) 2 - 2/t = 2

Answer 2

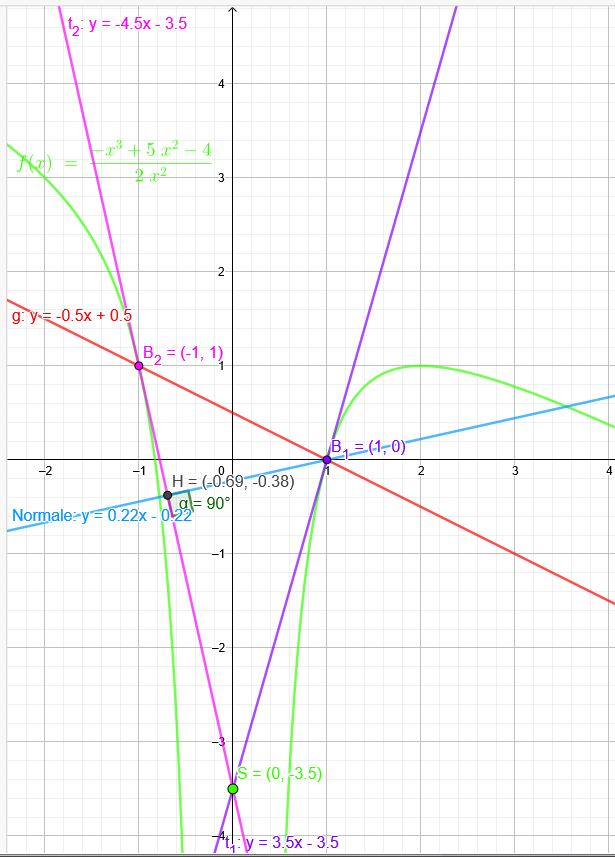
c) Vom Punkt S\((0|-3,5)\) lassen sich zwei Tangenten an die Kurve K legen. S und die beiden Berührpunkte sind Eckpunkte eines Dreiecks.

K:\(f(x)=\frac{-x^3+5x^2-4}{2x^2}\)

Ableitung mit der Quotientenregel:

\( [\frac{Z}{N}]'=\frac{Z'N-ZN'}{N^2} \)

\(f'(x)=\frac{(-3x^2+10x)2x^2-(-x^3+5x^2-4)4x}{4x^4}\)

\(f'(x)=\frac{8-x^3}{2x^3}\)

Die Berührpunkte auf K haben die Koordinaten B\((x|\frac{-x^3+5x^2-4}{2x^2})\)

Die Steigung zwischen S\((0|-3,5)\) und dem Berührpunkt B \((x|\frac{-x^3+5x^2-4}{2x^2})\), muss gleich der Steigung im Berührpunkt sein.

\( \frac{\frac{-x^3+5x^2-4}{2x^2}-(-3,5)}{x-0}=\frac{8-x^3}{2x^3} \)

\( \frac{\frac{-x^3+5x^2-4}{2x^2}+3,5}{x}=\frac{8-x^3}{2x^3} \)
Multiplikation "Überkreuz"

\( x_1=0\) ist nicht definiert

\( x_2=1\)       \(f(1)=\frac{-1+5-4}{2}=0\)

1.Tangente :  \(f'(1)=\frac{8-1}{2}=3,5\)

\(B_1(1|0)\)    und S\((0|-3,5)\)

\( \frac{y-(-3,5)}{x}= 3,5\)

1.) \( y= 3,5x-3,5\)

\( x_3=-1\)     \(f(-1)=1\)

2.Tangente : \(f'(-1)=\frac{8+1}{-2}=-4,5\)

\( \frac{y-1}{x+1}=-4,5 \)

2.)  \( y=-4,5x-3,5 \)

Berechnen Sie den Flächeninhalt.

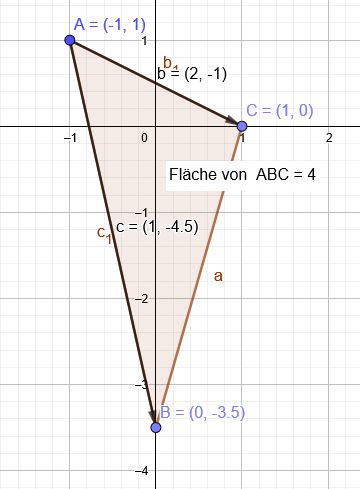
\(\vec{b} =\begin{pmatrix} 2\\-1\\ \end{pmatrix}\)  und \(\vec{c} =\begin{pmatrix} 1\\-4,5\\ \end{pmatrix}\)

\( \begin{pmatrix} 2 & 1 \\ -1 & -4,5 \end{pmatrix} \)

Dreiecksfläche: (Vektorprodukt)

\(2A=|2\cdot(-4,5)|-|1\cdot(-1)|=8\)

\(A=4\)FE