Obersumme und Untersumme, wie berechnen?

Question

Aufgabe:

Funktion lautet f(x)=X²

1) Gib die Teilintervallgrenzen ti, i=0...n, bei einer äquidistanten Zerlegung des Intervalls (0;2) in n=4 Teilintervalle an (Untersumme, U4)

to=0. t1=...

2) Rechne die Obersumme O4 aus.

3) Gib die Teilintervallgrenzen ti, I=0..n, bei einer äquidistanten Zerlegung des Intervalls (1;2) in n=8 Teilintervalle an.

to=1, t1=...

Problem/Ansatz:

Ich weiß einfach gar nicht wie ich vor gehen soll. Unser Lehrer hat uns einfach 3 Arbeitsblätter gegeben, die das erklären sollen. Aber ich verstehe leider nichts

Answer 1

hallo

f(x)=x^2  Untersumme für 4 Unterteilungen von 0 bis 2 Unterteilung :t0=0, t1=1/2, t2=1, t3=3/2

t4=2

jetzt  Untersumme: 1/2*(0^2+(1/2)^2+1^2+(3/2)^2)

Obersumme :1/2*(1/2)^2+1^2+(3/2)^2+2^2 )

Untersumme grün, Obersumme braun

lul

Comments

Dankeschön. Könntest du mir bitte verraten, wie man Aufgabe 3 berechnet?

Answer 2

Hallo,

1. Untersumme

Wenn du das Intervall von 0 bis zwei in vier gleich breite Teilintervalle teilst, haben diese alle die Breite 0,5. Die Höhe der entsprechenden Rechtecke entspricht bei der Untersumme dem kleineren Funktionswert.

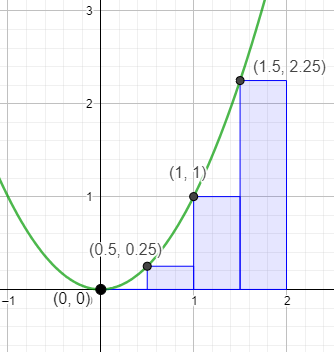
Du hast also vier Rechtecke mit dem Gesamtinhalt von \(0\cdot0+0,5\cdot0,25+0,5\cdot 1+0,5\cdot 2,25=0,125+0,5+1,125=1,75\) oder einfacher \(0,5\cdot(0+0,25+1+2,25)=1,75\).

2. Zur Berechnung der Obersumme gehst du analog vor, nur entsprechen die Höhen der Rechtecke dem höheren Funktionswert.

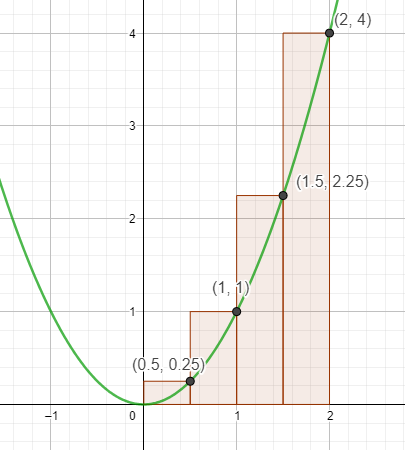
\(0,5\cdot(0,25+1+2,25+4)=3,75\)

3. Bei der Unterteilung des Intervalls in acht gleich große Teilintervalle sind die Grenzen

1 1,125 1,25 1,375 1,5 1,625 1,75 1,875 2

Gruß, Silvia

Comments

Hey Silvia, dankeschön. Super erklärt. Wäre die Untersumme bei Aufgabe 3) 2,148?

---

Sehr gut, das ist richtig.

---

Und kommt bei der Obersumme dann 2,5229 raus?

---

"Geogebra" kommt auf 2,5234, aber auf 4 Stellen dem Komma zu berechnen, finde ich ungwöhnlich, 2 sollten reichen.

---

Ohja, ich hab da wohl etwas zu viel gerundet. Aber vielen Dank. Sie haben mir echt geholfen. Eigentlich wollte ich Ihnen den Stern geben, aber ich hab mich verklickt.... tut mir leid

---

Das ist gar kein Problem. Hauptsache, du hast es verstanden.