Wachstumsgeschwindigkeit v berechnen

Question

Aufgabe:

Spiralblume

Die Wachstumsgeschwindigkeit v einer Spiralblume (flos helica) wurde in einer Graphik erfasst (t in Tage, v in cm/Tag).

a) Modellieren Sie v durch eine quadratische Funktion.

b) Zu Beginn der 3-tägigen Wachstums- periode ist die Blume 1m hoch. Wie hoch ist sie am Ende der Periode?

c) Wann ändert sich die Höhe nur noch um I cm/Tag? Wie hoch ist die Blume dann?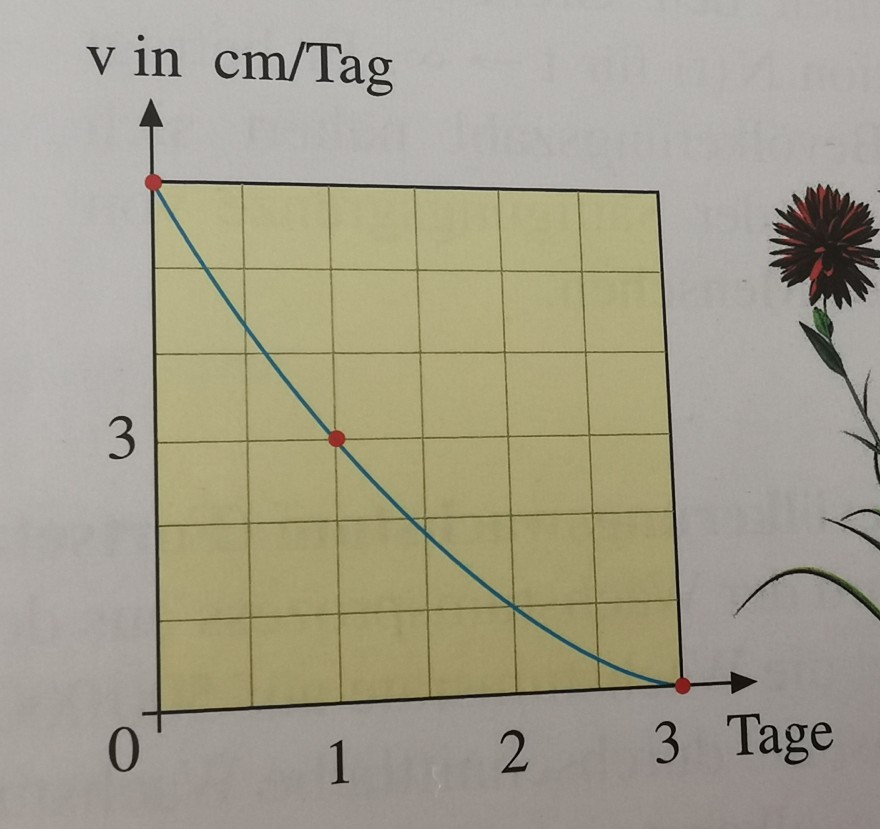

Problem/Ansatz:

rekonstruktion der funktion??

v(t) = ax^2 + bx + c

a) (I)  f(0) = 5

   (II) f(1) = 3

   (III) f(3) = 0

Answer 1

v(t) = ax² + bx + c

a) (I)  f(0) = 6

(II) f(1) = 3

(III) f(3) = 0

also: c=6

(1) 3=a+b+6

(2) 0=9a+3b+6

Dies System kannst du sicher lösen.

Comments

Zur Kontrolle:

Funktionsgleichung zu a) v(t)=0,5t²-3,5t+6

Funktionsgleichung zu b) V(t)=x³/6-7x²/4+6x+1.