Hallo Botaniker,
Ein paar Dinge sind noch unklar. Aus Deiner Frage entnehme ich, dass der Roboter zwar vier Räder hat, aber nicht über eine Lenkung gesteuert wird, sondern (wie ein Panzer) indem die Räder (alle Räder!) auf den beiden Seiten mit unterschiedlichen Drehzahlen angesteuert werden. Das bedeutet natürlich, dass die Räder dann wegrutschen, d.h. nicht in einer Spur bleiben.
Auf dem Bild, das Du verlinkt hast, ist ein Lego-Fahrzeug zu sehen. So weit ich das beurteilen kann, hat dieses Fahrzeug eine Lenkung und die gelenkten Räder haben keinen(!) Antrieb.
Nehmen wir trotzdem mal an, dass die Räder fest sind (ungelenkt) und alle Räder angetrieben werden und Räder einer Seite über ein Getrebe o.ä. verbunden sind, so dass beide immer gleich drehen. Dann betrachte ich den Fall, bei dem die Räder der beiden Seiten genau gegenläufig mit gleicher Drehzahl angesteuert werden. Dann sollte sich der Roboter auf der Stelle drehen.
Ja und dann nehme ich noch an, dass sich der Schwerpunkt in der Mitte (bezogen auf die Räder) des Fahrzeugs befindet. Ich vermute, dass sich das Fahrzeug immer um den Schwerpunkt drehen würde, solange dieser sich auf der Mittellinie des Fahrzeugs befindet!
Nach dem ganzen Vorgeplänkel ergibt sich folgendes Bild:
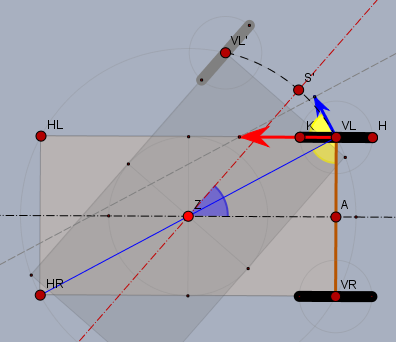
Ich erkläre dass Modell an Hand des linken Vorderrades (Punkt \(V_L\)). Das Fahrzeug steht so, dass es in Geradeausfahrt nach rechts fahren würde. Der Radstand des Fahrzeugs sei \(a=2|ZA|\) und seine Spurweite sei \(b=2|AV_L|\). Die Fahrzeugmitte und der Schwerpunkt liege im Punkt \(Z\).
Soll sich das Fahrzeug um den Winkel \(\alpha\) (blau) drehen, so muss das Vorderrad in die Position \(V_L'\) (das graue Rad). Dazu legt der Berührpunkt des Rades auf dem Boden den gestrichelten schwarzen Kreisbogen der Länge \(k\) zurück. $$k = \frac 12\sqrt{a^2+b^2} \cdot \alpha$$Dreht das Rad aber nach links (der rote Pfeil), so kann davon nur der Weg genutzt werden, der tangential zum Kreisbogen verläuft (der blaue Pfeil). Sei der gelbe Winkel \(\varphi\), so ist der Weg des Rades um \(1/\cos(\varphi)\) länger. Und $$\cos(\varphi) = \frac{2|AV_L|}{|V_LH_R|} = \frac {b}{\sqrt{a^2+b^2}} $$so ist der Weg \(s\), den das Rad zurücklegen muss$$s = \frac k{\cos(\varphi)} = \frac 12 \frac{\sqrt{a^2+b^2}}{\frac {b}{\sqrt{a^2+b^2}}} \cdot \alpha = \frac b2\left(\left(\frac ab\right)^2 +1\right) \alpha$$und der gesuchte Drehwinkel \(\Theta\), den sich die Räder drehen müssen, ist natürlich vom Radius \(r\) der Räder abhängig:$$\Theta = \frac sr = \frac b{2r}\left(\left(\frac ab\right)^2 +1\right) \alpha$$das wäre die Theorie, mit den ganzen Annahmen, die ich oben gemacht habe. In der Praxis wird dieser Wert eher eine untere Grenze darstellen. Die Räder werden beim Beschleunigen (also Anfahren) bereits durchrutschen ohne dass die Drehbewegung der Räder in eine Drehung des Fahrzeugs umgesetzt werden kann.
Weiter ist das Mass \(b\) der (wirksamen) Spurweite auch davon abhängig, ob die Räder einen gewissen Schrägstand haben. Somit kann \(b\) nochmal um die Radbreite schwanken. Und es gibt bestimmt noch mehr Sachen, an die ich jetzt nicht gedacht habe ;-)
Probier's einfach aus. Lass die Räder drehen und mache eine Messreihe mit unterschiedlichen Werte und wiederhole die Messungen auch.
Wäre toll wenn Du uns dann ein kleines Feedback gibst.
Gruß Werner