Aufgabe:
Untersuchen Sie die folgenden Reihen auf Konvergenz und absolute Konvergenz.
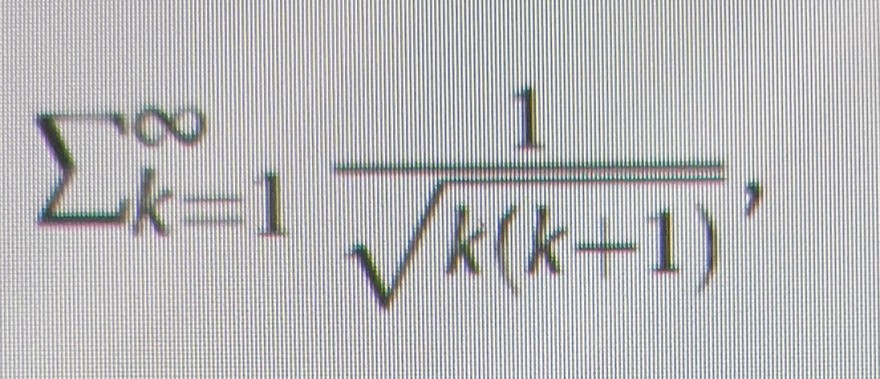
Text erkannt:
\( \sum \limits_{k=1}^{\infty} \frac{1}{\sqrt{k(k+1)}} \)
Das ist meine Lösung. Wenn das falsch ist, kann jemand das dür mich korrgieren oder eine andere Weg zu zeigen? Vielen Dank im Voraus.

Text erkannt:
\( \sum \limits_{k=1}^{\infty} \frac{1}{\sqrt{k(k+1)}} \)
\( \lim \limits_{k \rightarrow \infty} S_{n}=\lim \limits_{k \rightarrow \infty} \sum \limits_{k=1}^{\infty} \frac{1}{\sqrt{k(k+1)}}=0 \) endlich
Die Reihe konvergient zu null.
Untersuchurg der Absolut:
1. Schritt: suche nach \( \left|a_{k}\right| \)
\( \begin{array}{c} \lim \limits_{k \rightarrow \infty}\left|a_{k}\right|=\lim \limits_{k \rightarrow \infty} \sum \limits_{k \rightarrow 1}^{\infty}\left|\frac{1}{\sqrt{k(k+1)}}\right| \\ =\lim \limits_{k \rightarrow \infty} 0 \frac{1}{\sqrt{k(k+1)}}=0 \end{array} \)
Die Reihe ist monoton fallend \( \Rightarrow \) Konvergiert
2. Schritt \( \sum \limits_{k=1}^{\infty}=\sum \limits_{k=1}^{\infty}\left(a_{k}\right) \)
\( \sum \limits_{k=1}^{\infty} \frac{1}{\sqrt{k(k+1)}} \)
Be dor asile Schritt istes fallend. Also es Konvengient.