Berechnung mit Geradenscharen in einer Pyramide mit Lösungsansatz. Wäre sehr dankbar!

Question

Aufgabe:

Die Geradenschar g(a): x = (0/-4/8) + s*(1/2/a) beschreibt den Verlauf eines Lasers, der im Rahmen einer Laser-Show auf das Kantenmodell einer Pyramide trifft (s.Abb.). Untersuchen sie, wo einzelne Laserstrahlen die Kanten der Pyramide treffen.

Problem/Ansatz:

Kann mir bitte einer beim Ansatz für die Bearbeitung dieser Aufgabe helfen? Ich verstehe nicht inwiefern ich diese Aufgabe lösen. Ein ausführlichen Lösungsweg als Beispiel von einer Kante wäre auch sehr hilfreich.

Text erkannt:

c) Die Geradenschar \( g_{a} \) aus Aufgabe a) beschreibt den Verlauf eines Lasers, der im Rahmen einer Laser-Show auf das Kantenmodell einer Pyramide trifft (s. Abb.). Untersuchen Sie, wo einzelne Laserstrahlen die Kanten der Pyramide treffen.

Answer 1

Hallo,

stelle die Gleichung der Geraden durch B und S auf.

\(g:\;\vec{x}=\begin{pmatrix} 4\\4\\0 \end{pmatrix}+r\cdot\begin{pmatrix} -2\\-2\\5 \end{pmatrix}\)

und setze sie = der Geradenschar

\(\begin{pmatrix} 4\\4\\0 \end{pmatrix}+r\cdot\begin{pmatrix} -2\\-2\\5 \end{pmatrix}=\begin{pmatrix} 0\\-4\\8 \end{pmatrix}+s\cdot \begin{pmatrix} 1\\2\\a\end{pmatrix}\)

Das ergibt das Gleichungssystem

4 - 2r = s

4 - 2r = -4 + 2s

5r = 8 + as

Die ersten beiden Gleichungen ergeben s = -4 + 2 s ⇒ s = 4

Setze 4 für s in die 1. Gleichung ein ⇒ r = 0

Eingesetzt in die 3. Gleichung ergibt

-a·4 = 8 ⇒ a = -2

So kannst du auch bei den anderen Kanten vorgehen.

Gruß, Silvia

Comments

Vielen Dank für die Hilfe

---

ein Bild sagt mehr als tausend Worte:

(klick drauf)

---

Besonders dann, wenn es so gut gelungen ist!

---

Eine Frage: Muss jetzt als Antwort nun stehen bei einem Wert für a=-2 trifft der Laserstrahl die Kante zwischen B und S?

---

Untersuchen Sie, wo einzelne Laserstrahlen die Kanten der Pyramide treffen.

Das verstehe ich so, dass du auch noch den Schnittpunkt zwischen Spot und Kante berechnen sollst.

---

In der Aufgabestellung steht:

Untersuchen sie, wo einzelne Laserstrahlen die Kanten der Pyramide treffen.

D.h. es ist nicht nach dem jeweiligen Wert von \(a\) gefragt. Es schadet natürlich nicht, ihn anzugeben.

Gefragt ist nach dem Punkten wo einer der Laserstrahlen das Kantenmodell trifft. Einen hat Dir Silvia vorgerechnet:$$s=4, \quad a=-2 \\\implies T_1 = \begin{pmatrix} 0\\-4\\8 \end{pmatrix}+4\cdot \begin{pmatrix} 1\\2\\-2\end{pmatrix} = \begin{pmatrix} 4\\4\\0 \end{pmatrix}$$und das ist die Ecke \(B\). Es fehlen noch zwei weitere Punkte auf den Kanten \(OA\) und \(AS\).

Überprüfe Deine Ergebnisse an Hand der Szene oben. Wenn Du auf das Bild klickst, kannst Du das Script für die Szene sehen und ggf. Deine Ergebnisse eintragen. Z.B. für den Punkt \(T_1\)

punkt(4|4|0 "T1")

---

Was ist genau gemeint mit es fehlen noch zwei weitere Punkte auf den jeweiligen Kanten. Sollte es das nicht schon gewesen sein für die Kante zwischen S und B. Heißt also es müssten nun die anderen 7 Kanten folgen

Und danke nochmal für die Antworten und besonders für die Darstellung weiß ich sehr zu schätzen:)

---

Werner hat geschrieben

Es fehlen noch zwei weitere Punkte auf den Kanten OA und AS

Die anderen Kanten werden, wie du anhand des Bildes sehen kannst, nicht von dem Laserstrahl getroffen.

---

Auch Kante AB nicht? Laut der Rechnung landet man auf den Eckpunkt B??

---

Bei Kante BC ist es genau das gleiche Prinzip

Hier meine Rechnung:

---

Auch Kante AB nicht? Bei Kante BC ist es genau das gleiche Prinzip

Wenn Du die Kanten \(AB\), \(BC\) oder \(BS\) rechnest landest Du immer beim Punkt \(B\). Denn ein Lasestrahl trifft \(B\) und \(B\) ist in jeder der Kanten enthalten.

Es fehlen aber noch die Kanten \(OA\) und \(AS\). Dort gibt es jeweils noch ein Treffer. (ich schrieb dies bereits s.o.)

Heißt also es müssten nun die anderen 7 Kanten folgen

Na ja, wenn man sich 'blind stellt' müsste man das tun. Aber Du könntest Dir auch eine Skizze machen. Und zwar nur die Projektion auf die \(x_1x_2\)-Ebene:

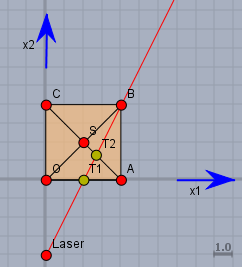
Du siehst hier die Szene von oben. Nach rechst geht die Richtung \(x_1\) und nach oben in der Zeichnung die Richtung \(x_2\).

Da der Parameter \(a\) nur die 'Höhe' des Strahls vorgibt, fallen in dieser Ansicht alle Geraden der Schar zu der roten Geraden zusammen. Nun sollte offensichtlich sein, dass es außer im Punkt \(B\) genau noch zwei weitere Punkte \(T_1\) (auf OA) und \(T_2\) (auf AS) im Kantenmodell gibt, die vom Laser getroffen werden. Und nur diese müssen gerechnet werden.

Noch eine Bemerkung: Wenn Du von irgendeiner der Kanten den Schnittpunkt mit dem Laser berechnest, so wirst Du in jedem(!) Fall einen Schnittpunkt erhalten. Ob der Schnittpunkt aber wirklich auf einer Kante liegt oder nicht, hängt von dem Parameter der Geradengleichung der Kantengeraden ab.

Beispiel: die Kante OA ist $$k_{OA}: \quad x = O + r\cdot(A-O) = \begin{pmatrix} 0\\ 0\\ 0\end{pmatrix} + r\begin{pmatrix} 4\\ 0\\ 0\end{pmatrix}$$In diesem Fall muss der Paraneter \(r\) zwischen 0 und 1 liegen (inklusive), damit die Kante auch getroffen wird. Liegt \(r\) außerhalb dieses Intervalls, gibt es auch keinen Treffer.

Insofern war es von Silvia ungünstig, den Parameter des Laserstrahls zu berechnen. Der muss lediglich \(\gt 0\) sein!

Überlege bitte selber, warum das so ist und klicke nochmal auf das Bild in meinem Kommentar. Dann öffnet sich Geoknecht3d und Du kannst die Szene mit der Maus rotieren. So bekommst Du einen besseren Eindruck.