Trigonometrische Funktion tan(4x)

Question

Aufgabe: Trigonometrische Funktion

Problem/Ansatz:

Guten Nachmittag,

Ich sollte di Identität der Trigonometrischen Funktion tan(4x) berechnen (siehe foto) und habe keine Ahnung wo oder wie ich mit der Rechnung beginnen soll.

Mfg, Mark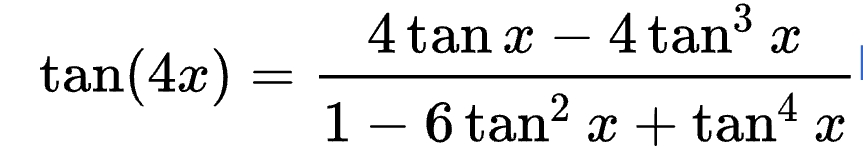

Text erkannt:

\( \tan (4 x)=\frac{4 \tan x-4 \tan ^{3} x}{1-6 \tan ^{2} x+\tan ^{4} x} \)

Answer 1

Mit den bekannten Additionstheoremen für \(\sin\) und \(\cos\) erhält man zunächst$$\tan(2x)=\frac{\sin(2x)}{\cos(2x)}=\frac{2\sin(x)\cos(x)}{\cos^2(x)-\sin^2(x)}=\frac{2\dfrac{\sin(x)}{\cos(x)}}{\hspace{6px}1-\dfrac{\sin^2(x)}{\cos^2(x)}\hspace{6px}}=\frac{2\tan(x)}{1-\tan^2(x)}.$$Ersetzt man \(x\) durch \(2x\), dann hat man demzufolge$$\tan(4x)=\frac{2\tan(2x)}{1-\tan^2(2x)}=\frac{2\dfrac{2\tan(x)}{1-\tan^2(x)}}{1-\left(\dfrac{2\tan(x)}{1-\tan^2(x)}\right)^2}=\frac{4\tan(x)\big(1-\tan^2(x)\big)}{\left(1-\tan^2(x)\right)^2-4\tan^2(x)}.$$Es folgt$$\large\boxed{\tan(4x)=\frac{4\tan(x)-4\tan^3(x)}{1-6\tan^2(x)+\tan^4(x)}}$$

Comments

Vielen Dank!!

Answer 2

Hallo,

tan (4x)= tan(2 *2x)

tan(2x)= (2 tan(x))/(1 -tan^2(x))

Comments

Vielen Dank!