Bestimmen Sie den Wert von u, für den der Flächeninhalt maximal wird, und geben Sie den maximalen Flächeninhalt an.

Question

Aufgabe:

Problem/Ansatz:

Text erkannt:

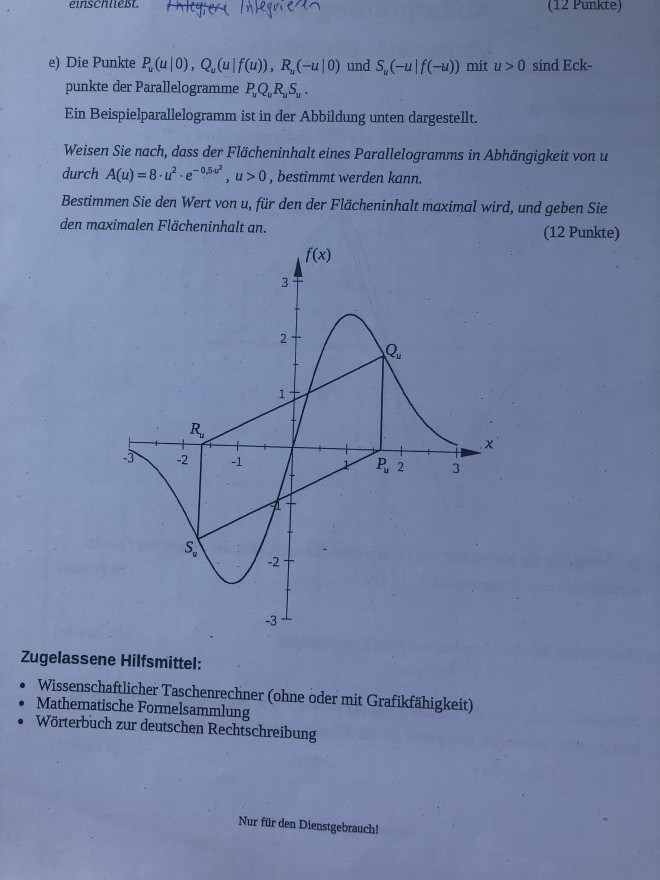
e) Die Punkte \( P_{u}(u \mid 0), Q_{u}(u \mid f(u)), R_{u}(-u \mid 0) \) und \( S_{u}(-u \mid f(-u)) \) mit \( u>0 \) sind Eckpunkte der Parallelogramme \( P_{u} Q_{u} R_{u} S_{u} \).
Ein Beispielparallelogramm ist in der Abbildung unten dargestellt.
Weisen Sie nach, dass der Flächeninhalt eines Parallelogramms in Abhängigkeit von \( u \) durch \( A(u)=8 \cdot u^{2} \cdot e^{-0.5 u^{2}}, u>0 \), bestimmt werden kann.

Bestimmen Sie den Wert von u, für den der Flächeninhalt maximal wird, und geben Sie den maximalen Flächeninhalt an.
(12 Punkte)
Zugelassene Hilfsmittel:
- Wissenschaftlicher Taschenrechner (ohne oder mit Grafikfähigkeit)
- Mathematische Formelsammlung
- Wörterbuch zur deutschen Rechtschreibung
Nur für den Dienstgebrauch!

Ich komme bei der letzten Aufgabe leider absolut nicht weiter. Hilfe wäre sehr erfreuenswert

Comments

Wie lautet die Funktionsgleichung von \(f\) ?

Answer 1

Hallo

A des Parallelogramms ist  durch 2*Fläche des Dreiecks R mit Kathete 2u und f(u)  also A=2u*f(u) gegeben (da f(x) offensichtlich punktsymmetrisch zu 0 ist)

das Max zu finden ist dann hoffentlich klar?

Gruß lul

Comments

Danke für die Hilfe!!!

---

Die Fläche besteht nicht nur aus zwei Dreiecken sondern ist auch ein Parallelogramm welches sich aus Grundseite mal Höhe berechnet. Grundseite hätte ich mit f(u) und die Höhe mit 2u gewählt.

---

Ist das nicht dasselbe? "Die Fläche besteht nicht nur aus zwei Dreiecken sondern ist auch ein Parallelogramm"

Answer 2

f(x) = 4·x·e^(-0.5·x^2)

A(u) = (2·u)·f(u) = (2·u)·(4·u·e^(-0.5·u^2)) = 8·u^2·e^(-0.5·u^2)

A'(u) = e^(- 0.5·u^2)·(16·u - 8·u^3) = 0 --> u = ±√2 (oder u = 0)

Für u = √2 wird die Fläche maximal und die Fläche Beträgt dann

A(u) = 8·(√2)^2·e^(-0.5·(√2)^2) = 16/e = 5.886 FE