a0 = 1/1 → 1=2^0
a1 = 1/2 → 2=2^1
a2 = 1/8 → 8=2^3
a3 = 1/16 → 16=2^4
Wir brauchen also eine Formel für folgende Zuordnung.
| Index k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Exponent | 0 | 1 | 3 | 4 | 6 | 7 | 9 | 10 | 12 |
Für gerade Indizes k ist es 1,5k.
Für ungerade Werte von k ist es 1,5(k-1)+1=1,5k-0,5.
Nun brauchst du nur noch einen Term, der für gerade Werte Null und für ungerade Werte 0,5 ergibt.
0,25 •(1-(-1)^{k})
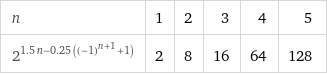
Also a_k = 2^{-1.5k+0.25(1-(-1)^k))