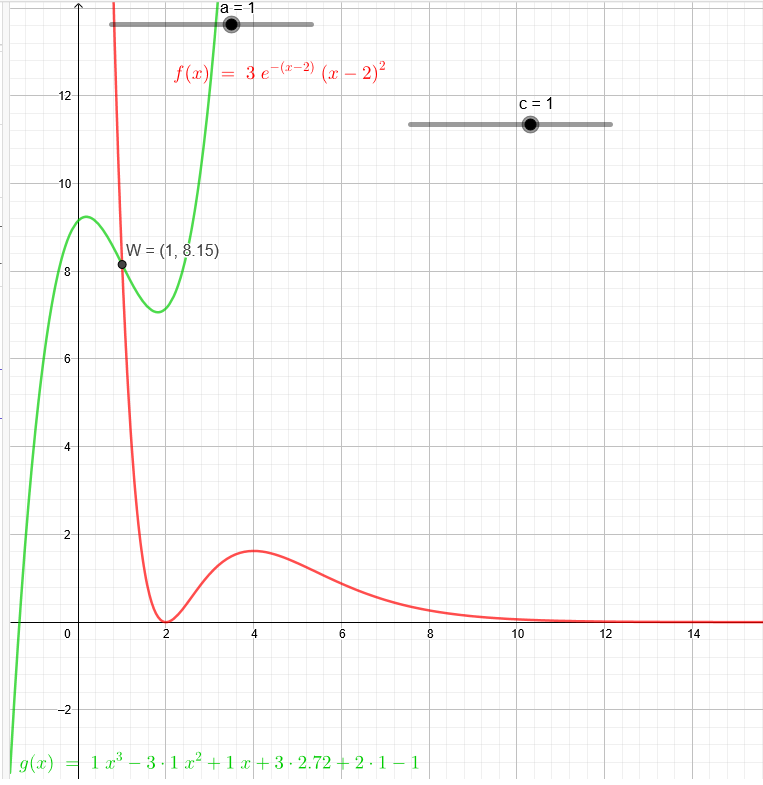
"Gegeben sei die Funktion \( j \) mit der Gleichung \( j(x)=3 \cdot e^{-(x-2)} \cdot(x-2)^{2}, x \in \mathbb{R} \). Der Graph dieser Funktion ist die Ortskurve der Wendepunkte einer weiteren Funktionenschar \( v_{k} \) mit \( k \in I R \). Geben Sie eine Funktionsgleichung dieser Funktionenschar \( v_{k} \) an."
\( j(x)=3 \cdot e^{-(x-2)} \cdot(x-2)^{2}, x \in \mathbb{R} \)
Wendepunkt bei: \(x=1\) \( j(1)=3 \cdot e^{-(1-2)} \cdot(1-2)^{2}=3*e\)
\(f(x)=a*x^3+b*x^2+c*x+d\)
\(f(1)=a+b+c+d\)
1.)\(a+b+c+d=3*e\)
\(f´(x)=3a*x^2+2b*x+c\)
\(f´´(x)=6a*x+2b\)
\(f´´(1)=6a+2b\)
2.) \(6a+2b=0\) \(b=-3a\) \(a-3a+c+d=3e\) \(d=3e+2a-c \)
\(f(x)=a*x^3-3a*x^2+c*x+3*2,718+2a-c\)