berechne die Beträge von Fp und Fn.

Question

\( \frac{a}{b} \) Aufgabe:

…

Gleitet ein Körper eine schiefe Ebene hinab ( die in der Skizze als Gerade dargestellt wird), so kann der auf ihn wirkende Schwerkraftvektor Fs in zwei Hilfsvektoren parallel und normal zur Ebene zerlegt werden, sodass Fs =Fp+Fn gilt. Die Bewegung des Körpers verläuft dann so, als gebe es keine Schwerkraft und es wirke lediglich die Kraft Fp auf ihn. Der Anstieg der Geraden, die die schiefe Ebene darstellt, ist k= -1/2, die Scherkraft ist Fs= (0|-12N).

a)Zeichne die Gerade, welche die schiefe Ebene darstellt, und den angegebenen Schwerkraftvektor in ein Koordinatensystem. Konstruiere die beiden Hilfsvektoren Fp und Fn.
GIb die Koordinaten der beiden Vektoren an.

b) berechne die Beträge von Fp und Fn. Um welchen Faktor ist der Betrag von Fp kleiner als jener von Fs?

c)Wie steil muss eine schiefe Ebene sein, damit ein hinabgleitender Körper in Bewegungsrichtung einer Kraft ausgesetzt ist, die nur halb so groß ist wie die Schwerkraft?

Problem/Ansatz:

Ich verstehe nicht wie man zu den Ergebnissen kommt.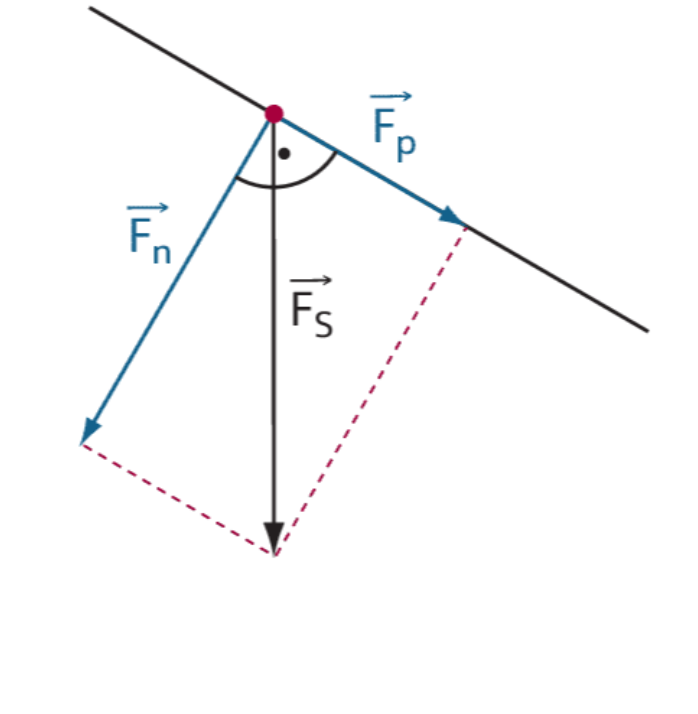

…

Answer 1

Zu (b)

Der Winkel der schiefen Ebene bezogen auf die Horizontale ist

\( \alpha = |\arctan(k) | = \left| \arctan \left( -\frac{1}{2} \right)  \right| = 26.565° \)

$$ \left| F_p \right| = \cos(90° - \alpha) \left| F_s \right| = 5.367 \ N $$

Und wegen \( \left| F_n \right|^2 + \left| F_p \right|^2 = \left| F_s \right|^2 \) folgt

$$ \left| F_n \right| = \sqrt{ \left| F_s \right|^2 - \left| F_p \right|^2 } = 10.733 \ N $$

Zu (c)

Es muss gelten $$ \cos(90° - \beta ) = \frac{ \frac{1}{2} \left| F_s \right| }{ \left| F_s \right| } = \frac{1}{2}  $$

Daraus ergibt sich

$$ \beta = 90° - \arccos \left( \frac{1}{2} \right) = 30° $$

Comments

Danke

und a?

---

A das Zeh Dir nicht abnehmen!

Ansonsten ist es so, der Vektor \( \vec{F_p} \) liegt auf der Geraden durch den Nullpunkt mit Steigung \( -\frac{1}{2} \) und deshalb liegt der Vektor \( \vec{F_n} \) auf einer Gearden durch den Nullpunkt mit Steigung \( 2 \).

D.h. der Vektor \( \vec{F_s} \) ergibt sich folgendermaßen

$$ \vec{F_s} = \alpha \vec{F_p} + \beta \vec{F_n} = \alpha \begin{pmatrix} 1 \\ 2  \end{pmatrix} + \beta \begin{pmatrix} 1 \\ -\frac{1}{2} \end{pmatrix} $$ mit noch zu bestimmenden Koeffizienten \( \alpha \) und \( \beta \).

Da \( \vec{F_s} = \begin{pmatrix} 0 \\ -12 \end{pmatrix} \) gilt, kann man das Gleichungssystem lösen und bekommt

$$ \alpha = \frac{24}{5} $$ und $$ \beta = -\alpha $$

Damit ergibt sich

\( \vec{F_n} = \frac{24}{5} \begin{pmatrix} 1 \\ -\frac{1}{2} \end{pmatrix} = \begin{pmatrix} 4.8 \\ -2.4  \end{pmatrix} \) und

\( \vec{F_p} = -\frac{24}{5} \begin{pmatrix} 1 \\ 2  \end{pmatrix} = \begin{pmatrix} -4.8 \\ -9.6  \end{pmatrix} \)