Bestimmen Sie die Wahrscheinlichkeit von :

Question

Aufgabe:

Seien A,B und C drei unabhängige Ereignisse mit P[A]=x, P[B]=y, P[C]=z. Bestimmen Sie die Wahrscheinlichkeit von :

A∩(BUC) (BUC : B vereint C)

Problem/Ansatz:

Hallo zusammen,

ich schreibe demnächst eine Stochastik Klausur und habe noch ein wenig Schwierigkeiten mit dem Thema Mengenlehre und Venn Diagramm.

Ich habe ein Venn Diagramm erstellt und bereits herausgefunden um welche Fläche es sich handelt.

Ich habe jetzt die folgende Menge aufgeschrieben, die (hoffentlich) auch alle Disjunkt sind:
A∩B∩C U (A∩B) ∩ (A∩B∩C)^c U (A∩C) ∩ (A∩B∩C)^c

^c: Komplement

Würdet ihr sagen, dass der Ansatz so stimmt und ich die Mengen in Wahrscheinlichkeiten umschreiben kann? Also P[A]=x, P[B]=y, P[C]=z einsetzen und berechnen?

Bei (A∩B∩C)^c muss ich wahrscheinlich die De-Morgansche Regel anwenden und hätte somit A^c U B^c U C^c

Bzw. würde ich die Aufgabe auch gerne in Mengenschreibweise ( Ohne Venn DIagramm) lösen. Leider fehlt mir da der Ansatz bzw ich bin mir dann nicht sicher, ob die Mengen dann auch stochastisch unabhängig sind.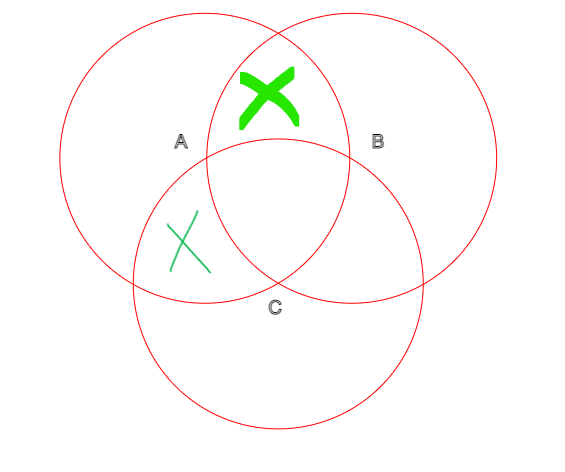

Ich wäre für jede Hilfe Dankbar!

Answer 1

\(\begin{aligned} & P\left(A\cap(B\cup C)\right) &  & \text{Distributivgesetz}\\ =\ & P\left(\left(A\cap B\right)\cup\left(A\cap C\right)\right) &  & \text{Siebformel}\\ =\ & P\left(A\cap B\right)+P\left(A\cap C\right)-P\left(A\cap B\cap C\right) &  & \text{Unabhängigkeit}\\ =\ & P\left(A\right)\cdot P\left(B\right)+P\left(A\right)\cdot P\left(C\right)-P\left(A\right)\cdot P\left(B\right)\cdot P\left(C\right)\\ =\ & xy+xz-xyz \end{aligned}\)

Comments

Hallo Oswald, vielen Dank für die Antwort!
Also darf ich die Siebformel auch bei so einer Art Formel berechnen? Also den Schnitt zweier Mengen als eine Menge betrachten?
Dürfte ich dann auch die Siebformel für:
(A∩B) U (A∩C) U (B∩C)

verwenden?

Natürlich dann die Siebformel für drei Mengen

---

Also den Schnitt zweier Mengen als eine Menge betrachten?

Was glaubst du, was der Schnitt zweier Mengen ist?

1. ein Kühlschrank
2. eine Menge
3. ein pharmazeutisch-technischer Assistent
   
4. eine Weintraube
   

Tipp. nur eine der vorgeschlagenen Antworten ist richtig.