Gegeben sei ein Spat mit den Kantenvektoren:
a= -2, 0, 0 b=0, -1, 3 c=3, 1, 0
a) Fertigen Sie eine Skizze des Spates an.
Das kannst du doch selbst. Zur Kontrolle:
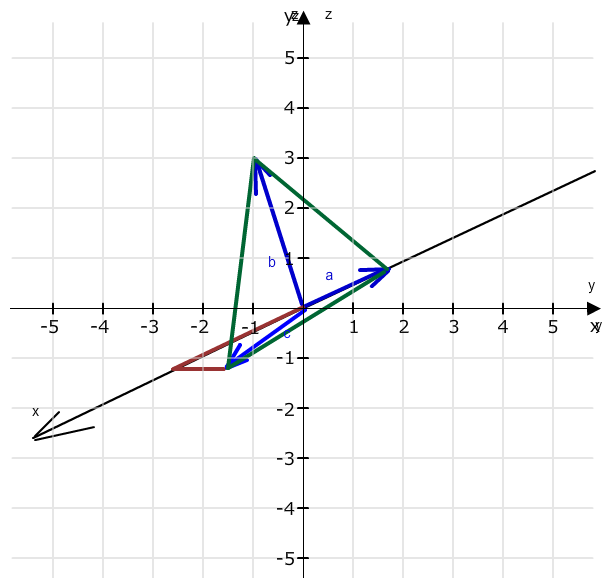
Jetzt im Schrägbild noch alle Dreiecke zu Parallelogrammen ergänzen.
b) Berechnen Sie einen Einheitsvektor parallel zu einer beliebigen Raumdiagonaler
Eine der Raumdiagonalen hat die Richtung (1,1,1)
Damit der Vektor ein Einheitsvektor ist noch durch die Länge teilen.
d = 1/√3 (1,1,1)
c) Berechnen Sie vektoriell den Winkel zwischen den Vektoren a und b .
a= -2, 0, 0 b=0, -1, 3
Skalarprodukt benutzen:
cos PHI = a*b / (|a|*|b|) = (0+0+0) / (2 * √10) = 0
PHI = 90°
d) Berechnen Sie vektoriell die Größe der von a und b aufgespannten Spatfläche
Vektorprodukt 'x' verwenden:
F = | (a x b) | = | ( 0-0 , -(-6-0) , 2-0) | = | (0,6,2)| = √(36+4) = 2*√10
e) Berechnen Sie vektoriell das Volumen des Spates
V = |Spatprodukt|
= | (a x b) * c|
= | (0,6,2) * (3,1,0) |
= | 6 |
= 6.