Zeigen Sie anhand einer Wahrheitstafel, dass die folgenden aussagenlogischen Formeln Tautologien sind:

Question

Aufgabe 3. Seien \( P \) und \( Q \) aussagenlogische Formeln. Zeigen Sie anhand einer Wahrheitstafel, dass die folgenden aussagenlogischen Formeln Tautologien sind:
1. \( P \leftrightarrow \neg(\neg P) \).
2. \( \neg(P \wedge Q) \leftrightarrow(\neg P \vee \neg Q) \).
3. \( ((P \rightarrow Q) \wedge \neg Q) \rightarrow \neg P \).

Comments

Mach doch mal einen Vorschlag, den wir dann ggf. korrigieren können.

Answer 1

In der Aufgabe ist doch bereits exakt vorgegeben, wie du vorgehen sollst.

Du sollst eine Wahrheitstafel aufstellen. Was kannst du daran nicht?

Wenn du nicht weißt, wie das geht, könnte der Artikel https://de.wikipedia.org/wiki/Wahrheitstabelle evtl. weiterhelfen. Dort ist auch vorgemacht, wie man so eine Tabelle evtl. ausfüllt.

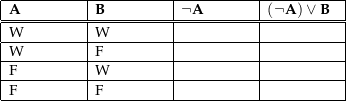
Du sollst das jetzt zwar mit P und Q anstatt mit A und B machen, aber das kann ja nicht viel schwerer sein, oder?