Aufgaben, bei denen das Einschalten eines digitalen Werkzeugs nicht wirklich hilft
wohl aber das Einschalten des Gehirns
Aufgabe 1: Das Parallelogramm ABCD liegt mit der Seite (BC ) ̅auf dem Durchmesser eines Kreises K mit dem Radius 5 cm. Die Seite (AB ) ̅ hat die Länge 6 cm und A liegt auf K. AD schneidet K in E. Wie lang ist (AE ) ̅?
Aufgabe 2: Wenn a-1/a=√6, was ist dann a4+1/a4 ?
Aufgabe 3: Wenn 2x+2,5y+3z=7 und 3x+6y+9z=15, was ist dann der kleinstmögliche Wert für x+y+z?
Aufgabe 4: Bestimme a in der Gleichung √(3+√a) -√(3-√a) =2.
Aufgabe 5: Drei Rennautos liefern sich ein Rennen mit unterschiedlichen konstanten Geschwindigkeiten und gleichzeitigem Start. Als der Sieger das Ziel passiert, liegt der Zweite 600 m und der Dritte 1000 m zurück. Als der Zweite die Ziellinie passiert, hat der Dritte noch 450 m zu fahren. Wie lang ist die Rennstrecke?
Aufgabe 6: Welcher Punkt auf der y-Achse hat von der Geraden mit der Gleichung y=x/2 den Abstand √5?
Aufgabe 7: ABCD sei ein Quadrat. Der Punkt E liege auf (AB ) ̅ und der Punkt F auf einer Verlängerung von (\overline{BC}) ̅ über C hinaus. Es gelte |(AE ) ̅ |=|(CF ) ̅ | und |(EF ) ̅ |=11∙√2. Wie lang ist (DF ) ̅?
Aufgabe 8: Wenn a=√6+1 und b=√6-1, was ist dann a/b+b/a?
Aufgabe 9: Es sei x-y=5. Gesucht ist dann der Wert des Bruches (x2-y2+6x+9)/(x2-y2+3x-3y).
Aufgabe 10: Zwei gleichlange Kerzen werden gleichzeitig angezündet. Die eine ist nach 10 Stunden, die andere nach 12 Stunden abgebrannt. Nach welcher Brenndauer betrug das Längenverhältnis 2:3?
Aufgabe 11: Es sei 3x=8 und 2y=9. Welchen Wert hat das Produkt x·y?
Aufgabe 12: Eine Klasse mit 30 Schüler*innen konnte zwischen den Fremdsprachen Englisch und Französisch wählen. Es war auch möglich, beide Sprachen zu wählen. Zählt man die Doppeltwähler*innen in allen Fällen mit, so wählten doppelt so viele Schüler*innen Englisch wie Französisch und viermal so viele wie Doppeltwähler*innen wählten Englisch. Wie viele Schüler*innen wählten Englisch?
Lösungen
Lösung Aufgabe 1: Nach Thales ist ABC ein rechtwinkliges Dreieck und nach Pythagoras ist dann |(AC ) ̅ |=8. ABC und AFC stimmen in allen Winkeln überein und sind folglich ähnlich. Dann gilt 6/10=|(AF ) ̅ |/8. Dann ist |(AF ) ̅ |=4,8 und 4,82+a2=25. Folglich ist a=1,4 und (AE ) ̅=2,8.

Lösung Aufgabe 2: Quadrieren der gegebenen Gleichung ergibt auf der linken Seite das gemischte Glied 2 und insgesamt a2-2+1/a2 =6 bzw. a2+1/a2 =8. Nochmaliges Quadrieren ergibt auf der linken Seite wiederum das gemischte Glied 2 und sonst a4+2+1/a4 =64 bzw. a4+1/a4 =62.
Lösung Aufgabe 3:
2x+2,5y+3z=7 |ˑ2
6x+6y+9z=15 |:(-3)
________________
4x + 5y + 6z= 14
–x – 2y – 3z = –5
addieren
3x + 3y + 3z = 9 |:3
x + y + z = 3
Jede Summe x + y + z ist gleich 3, also auch die kleinste.
Lösung Aufgabe 4: Für 0≤a≤9 ist √(3+√a) -√(3-√a) >0.
√(3+√a) -√(3-√a) =2 quadrieren:
3+√a - 2∙√((3+√a)(3-√a))+3-√a=4,
6+2∙√((3+√a)(3-√a))=4,
√((3+√a)(3-√a))=-1.
Nochmal quadrieren und 3. binomische Formel:
9-a=1 und a=8. Da 0<8<9 liegt a in einem Bereich, in dem beim Quadrieren die Lösung nicht verändert wird.
Lösung Aufgabe 5: Auf den letzten 600 m vor dem Zieleinlauf des Zweiten vergrößert sich sein Vorsprung vor dem Dritten von 400 auf 450 m, also um 50 m. Da beide mit konstanter Geschwindigkeit fahren, war und bleibt das während der gesamten Strecke so. Wenn s die gesuchte Streckenlänge ist, dann fährt der Zweite 9 Vorsprünge zu je 50 m auf 9ˑ600 m heraus, um im Ziel einen Vorsprung von 450 m zu haben. Also gilt s=5,4 km.
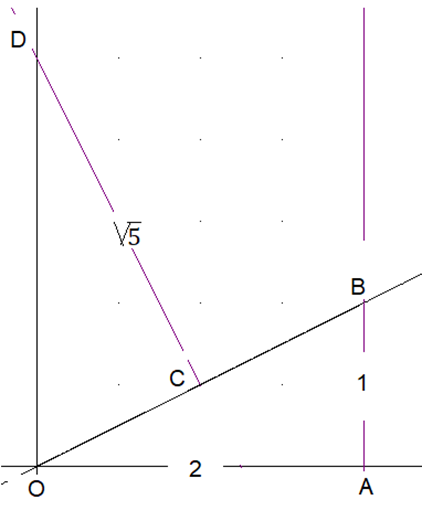
Lösung zu Aufgabe 6:
Im rechtwinkligen Dreieck OAB ist |(OB ) ̅ |=√5 Die Dreiecke OAB und OCD stimmen in allen Winkelgrößen überein und sind folglich ähnlich.
Dann gilt √5/2=|(OD ) ̅ |/√5 und dann
|(a ) ̅ |=5/2. Der gesuchte Punkt heißt D(0|2,5).
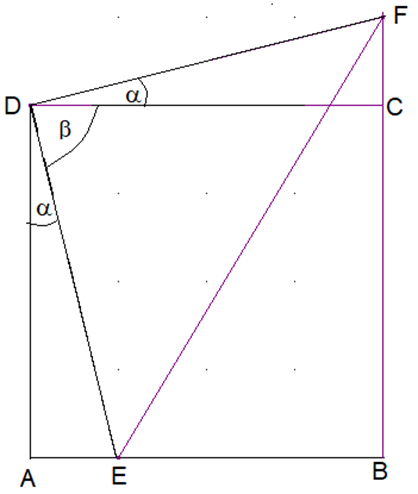
Lösung Aufgabe 7:
Die Dreiecke AED und DCF stimmen in den rechten Winkeln und den Kathetenlängen überein, sind also kongruent. α+β=90° also ist DEF ein gleichschenklig-rechtwinkliges Dreieck. Da dessen Hypotenuse die Länge 11∙√2 hat, ist die Kathete |(DF ) ̅ |=11.
Lösung Aufgabe 8:
(√6+1)/(√6-1)+(√6-1)/(√6+1)=((√6+1)2+(√6-1)2)/((√6+1)∙(√6-1) )=(6+2√6+1+6-2√6-1)/(6-1)=14/5.
Lösung Aufgabe 9:
(x2-y2+6x+9)/(x2-y2+3x-3y)=((x2+6x+9)-y2)/((x2-y2 )+(3x-3y) )=((x+3)2-y2)/((x-y)(x+y)+3(x-y) )=.
((x+3)-y)((x+3)+y)/(x-y)(x+y+3) =((x-y)+3)(x+3+y)/(x-y)(x+3+y) =(8(x+y+3))/(5(x+y+3)) =8/5.
Lösung Aufgabe 10:
Darstellung des Abbrennens im Weg-Zeit-Diagramm:
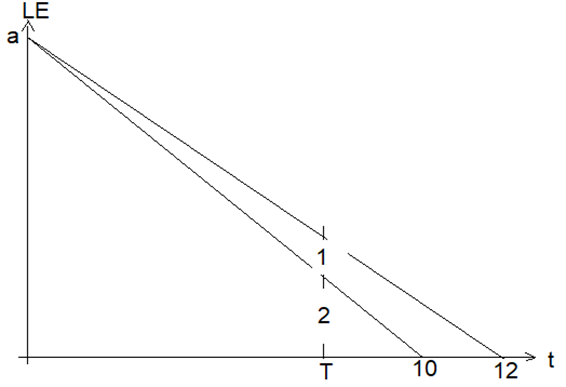
Die zugehörigen Funktionen sind
f(t)=a-a/10 t und
g(t)=a-a/12 t. Gesucht ist derjenige Zeitpunkt T, für den gilt (f(T))/(g(T))=2/3. Einsetzen der Funktionsterme: (a-a/10 T)/(a-a/12 T)=2/3. Ausklammern und Kürzen von a: (1-1/10 T)/(1-1/12 T)=2/3. Über Kreuz multiplizieren: 3∙(1-T/10)=2∙(1-T/12). Klammern auflösen und zusammenfassen: 1=3T/10-2T/12. Durchmultiplizieren mit 30: 30=9T-5T und schließlich T=7,5. Nach 7 ½ Stunden Brenndauer haben die Kerzen das Längenverhältnis 2:3.
Lösung Aufgabe 11:
Wegen 8=23 gilt 3x=23. Auf beiden Seiten mit y potenzieren:
(*) 3x∙y=23∙y. Wegen 2^(3∙y)=(2y )3 kann man jetzt 2y=9 in (*) einsetzen:
3x∙y=93 )oder 3xy=(32 )3. Dann ist 3x∙y=36 und x∙y=6.
Lösung Aufgabe 12:
Die Anzahl der Schüler*innen, die beide Sprachen wählten sei K.
Die Anzahl der Schüler*innen, welche Englisch wählten, sei E.
Die Anzahl der Schüler*innen, welche Französisch wählten, sei F.
Dabei ist K Teil von E wie von F. Dann entnimmt man dem Text:
(1) E + F – K = 30
(2) K=E/4
(3) F=E/2.
(2) und (3) in (1) einsetzen:
E+E/2-E/4=30 |∙4.
4E+2E-E=120 und E=24.