Aufgabe: In Aufgabe 2.c) sol für den vorgegebenen Richtungsvektor gezeigt werden,dass die Richtungsabletung im Punkt (0,0) existiert und diese dann auch berechnet werden.
Problem/Ansatz: Wenn man die Schnittfunktion h in die Funktion f einsetzt,erhält man ja eine relle Funktion die nur noch von t abhängt.Warum wird in den Lösungen nicht mit Hilfe des Differentenquotienten überprüft,ob die Funktion h im Punkt t=0 überhaupt differenzierbar 
Text erkannt:
Aufgabe 2
Vorgegeben sei die Funktion
\( f: \mathbb{R}^{2} \rightarrow \mathbb{R},(x, y) \mapsto f(x, y):=\left\{\begin{array}{cc} \frac{x \cdot y \cdot\left(e^{y}-1\right)}{x^{2}+y^{2} \cdot\left(e^{y}-1\right)^{2}}, & \text { falls }(x, y) \neq(0,0), \\ 0, & \text { falls }(x, y)=(0,0) . \end{array}\right. \)
(a) Ist die Funktion \( f \) im Punkt \( \left(x_{0}, y_{0}\right):=(0,0) \) partiell nach der Variablen \( x \) differenzierbar? Falls ja, so berechne man die partielle Ableitung.
(b) Ist die Funktion \( f \) im Punkt \( \left(x_{0}, y_{0}\right)=(0,0) \) partiell nach der Variablen \( y \) differenzierbar? Falls ja, so berechne man die partielle Ableitung.
(c) Es sei \( \vec{e}_{0}:=\frac{1}{\sqrt{2}} \cdot(1,1)^{\prime} \). Zeigen Sie, dass die Funktion \( f \) im Punkt \( \left(x_{0}, y_{0}\right)=(0,0) \) in Richtung des Vektors \( \vec{e}_{0} \) differenzierbar ist, und berechnen Sie \( \frac{\partial f}{\partial \vec{e}_{0}}(0,0) \).
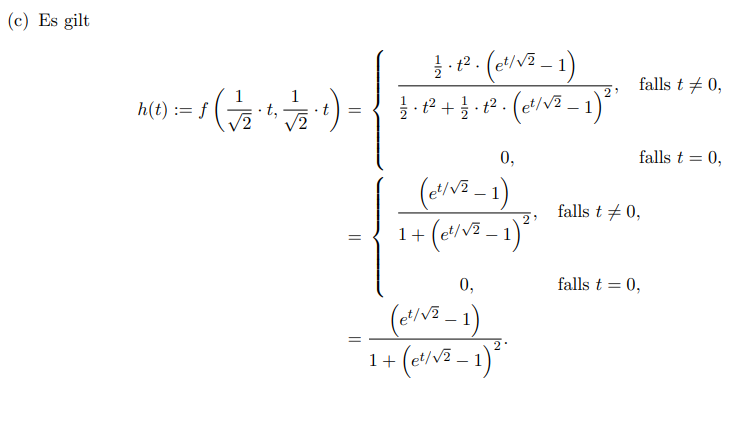
Text erkannt:
(c) Es gilt
\( h(t):=f\left(\frac{1}{\sqrt{2}} \cdot t, \frac{1}{\sqrt{2}} \cdot t\right)=\left\{\begin{array}{cc}\frac{\frac{1}{2} \cdot t^{2} \cdot\left(e^{t / \sqrt{2}}-1\right)}{\frac{1}{2} \cdot t^{2}+\frac{1}{2} \cdot t^{2} \cdot\left(e^{t / \sqrt{2}}-1\right)^{2}}, & \text { falls } t \neq 0 \\ 0, & \text { falls } t=0,\end{array}\right. \)
\( =\left\{\begin{array}{cc}\frac{\left(e^{t / \sqrt{2}}-1\right)}{1+\left(e^{t / \sqrt{2}}-1\right)^{2}}, & \text { falls } t \neq 0 \\ 0, & \text { falls } t=0\end{array}\right. \)
\( =\frac{\left(e^{t / \sqrt{2}}-1\right)}{1+\left(e^{t / \sqrt{2}}-1\right)^{2}} \).
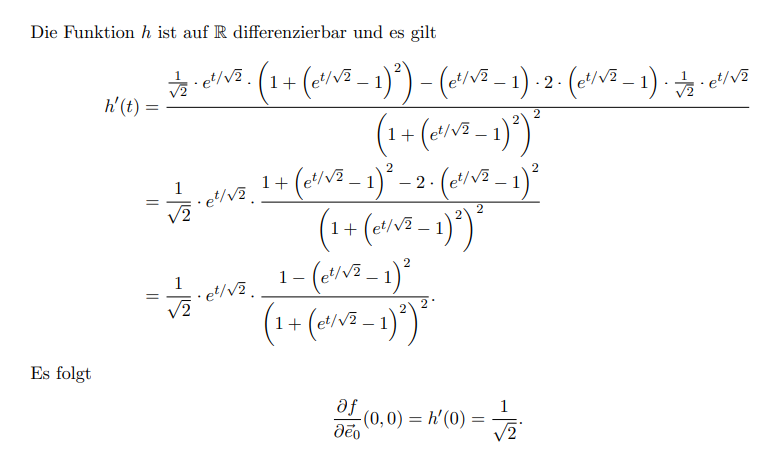
Text erkannt:
Die Funktion \( h \) ist auf \( \mathbb{R} \) differenzierbar und es gilt
\( \begin{aligned} h^{\prime}(t) &=\frac{\frac{1}{\sqrt{2}} \cdot e^{t / \sqrt{2}} \cdot\left(1+\left(e^{t / \sqrt{2}}-1\right)^{2}\right)-\left(e^{t / \sqrt{2}}-1\right) \cdot 2 \cdot\left(e^{t / \sqrt{2}}-1\right) \cdot \frac{1}{\sqrt{2}} \cdot e^{t / \sqrt{2}}}{\left(1+\left(e^{t / \sqrt{2}}-1\right)^{2}\right)^{2}} \\ &=\frac{1}{\sqrt{2}} \cdot e^{t / \sqrt{2}} \cdot \frac{1+\left(e^{t / \sqrt{2}}-1\right)^{2}-2 \cdot\left(e^{t / \sqrt{2}}-1\right)^{2}}{\left(1+\left(e^{t / \sqrt{2}}-1\right)^{2}\right)^{2}} \\ &=\frac{1}{\sqrt{2}} \cdot e^{t / \sqrt{2}} \cdot \frac{1-\left(e^{t / \sqrt{2}}-1\right)^{2}}{\left(1+\left(e^{t / \sqrt{2}}-1\right)^{2}\right)^{2}} . \end{aligned} \)
Es folgt
\( \frac{\partial f}{\partial \overrightarrow{e_{0}}}(0,0)=h^{\prime}(0)=\frac{1}{\sqrt{2}} \)
ist,sondern direkt behauptet,dass h in allen rellen Zahlen differenzierbar ist?