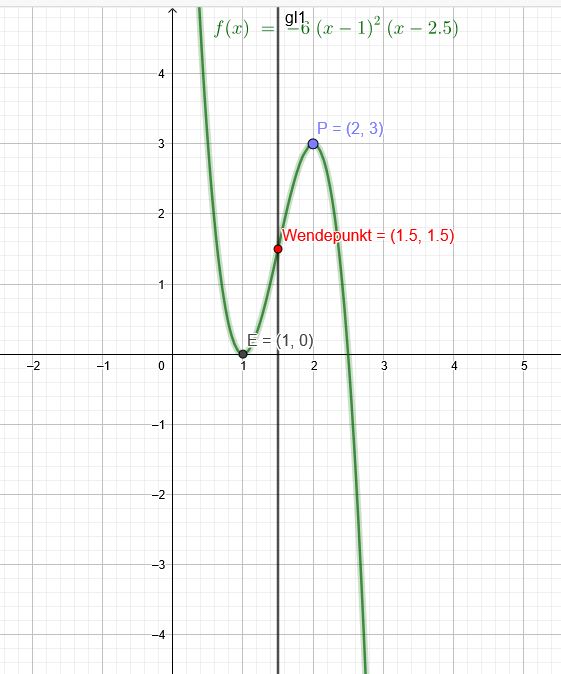
Bestimmen einer ganzrationalen Funktion mit gegebenen Punkt, Extremstelle und Wendestelle

Question

Aufgabe:

Bestimmen Sie eine ganzrationale Funktion, so dass (2|3) ein Punkt des Graphen, x = 1 eine
Extremstelle und x = 1,5 eine Wendestelle ist.

[Hinweis: Hier gibt es eine ganze Kurvenschar, die die Bedingungen erfüllt. Überprüfen Sie grafisch mit
GeoGebra, ob ihre Funktion die erforderlichen Eigenschaften immer erfüllt)

Problem/Ansatz:

Also ich hab alle Bedingungen Aufgeschrieben die mir eingefallen sind:

1. P(2/3) => f(2) = 3

2. Extremstelle = 1 =>f'(1)=0

3. Wendestelle = 1,5 => f''(1.5)=0

Und ich hab schon die Vermutung, dass es eine mindestens eine Funktion dritten Grades ist, aber ich weiß nicht wie ich mit den drei Gleichungen die ich habe 4 Unbekannte lösen kann.

Könnte mir bitte jemand ein Ansatz geben, wie man weiter kommen könnte?

Answer 1

Bestimmen Sie eine ganzrationale Funktion, so dass (2|3) ein Punkt des Graphen, x = 1 eine Extremstelle und x = 1,5 eine Wendestelle ist.

x = 1 eine Extremstelle. Ich lege nun diese Extremstelle auf die x-Achse → E(1|0) doppelte Nullstelle

f(x)= a*(x-1)²*(x-N)

P(2|3)

f(2)= a*(2-1)^2*(2-N)=a*(2-N)→ a*(2-N)=3  → $a=\frac{3}{2-N}$

$f(x)= \frac{3}{2-N}*[(x-1)^2*(x-N)]$

$f´(x)= \frac{3}{2-N}*[(2x-2)*(x-N)+(x-1)^2]$

$f´´(x)= \frac{3}{2-N}*[(2*(x-N)+(2x-2)+2*(x-1)]$

$f´´(1,5)= \frac{3}{2-N}*[(2*(1,5-N)+(3-2)+2*(1,5-1)]$

$\frac{3}{2-N}*[2*(1,5-N)+(3-2)+2*(1,5-1)]=0$      $N=2,5$    $a=\frac{3}{2-2,5}=-6$

$f(x)= -6*(x-1)^2*(x-2,5)$

Answer 2

Damit eine Wendestelle existieren kann,

muss es schon 3. Grades sein.

f(x)=ax³ + bx² + cx + d

f'(x) =3ax² + 2bx + c

f''(x) = 6ax + 2b

1. P(2/3) => f(2) = 3    ==>   8a+4b+2c+d=3

2. Extremstelle = 1 =>f'(1)=0==>   3a + 2b + c = 0

3. Wendestelle = 1,5 => f''(1.5)=0 ==>   9a + 2b = 0

8a+4b   +2c  +d=3
 3a + 2b + c       = 0
9a + 2b            = 0  ==> b=-4,5a

8a-18a   +2c +d=3
3a -9a + c       = 0

-10a + 2c + d = 3
-6a + c        =0      ==>   c= 6a

-10a +12a + d = 3 
                  d=3 -2a

Also erhält man die Schar:

f_a(x) = ax³ -4,5ax² + 6ax + 3 -2a

f_a'(x) = 3ax² -9ax + 6a

f_a''(x) =6ax -9a .

Nun noch die gegebenen Daten prüfen:

f_a''(1,5) =0 ✓ klappt für alle a.

f_a'''(x) = 6a ≠ 0 für a≠0, aber das

für Grad 3 ja gegeben sein.

Also wirklich Wendestelle bei 1,5.

f_a ' (1) = 0 ✓   f_a''(1)=-3a ≠0 , also wirklich

Extremstelle bei x=1.

f_a(2)=6a+3 . Das ist aber nur gleich 3, wenn a=0.

Also gibt es so eine Funktion 3. Grades nicht.

Kann höchstens mit höherem Grad klappen.

Comments

f_a(2)=6a+3

Nach meinen Berechnungen ist f_a(2)=3 unabhängig von a.

---

Na dann sieht es nat. anders aus.

Sorry, verrechnet.