wir haben vor kurzem mit der Binomialverteilung angefangen und ich verstehe diese mindestens, höchstens usw. nicht.
Bernoulli-Kette n = 11 ; Trefferwahrscheinlichkeit p = 0,43
Berechnen Sie die Wahrscheinlichkeiten für folgenden Ereignisse auf 5 Nachkommastellen:
C: höchstens 1 Niete (0.00145)
D: mindestens 1 Treffer (0.99794)
E: weniger als 2 Nieten (0.00145)
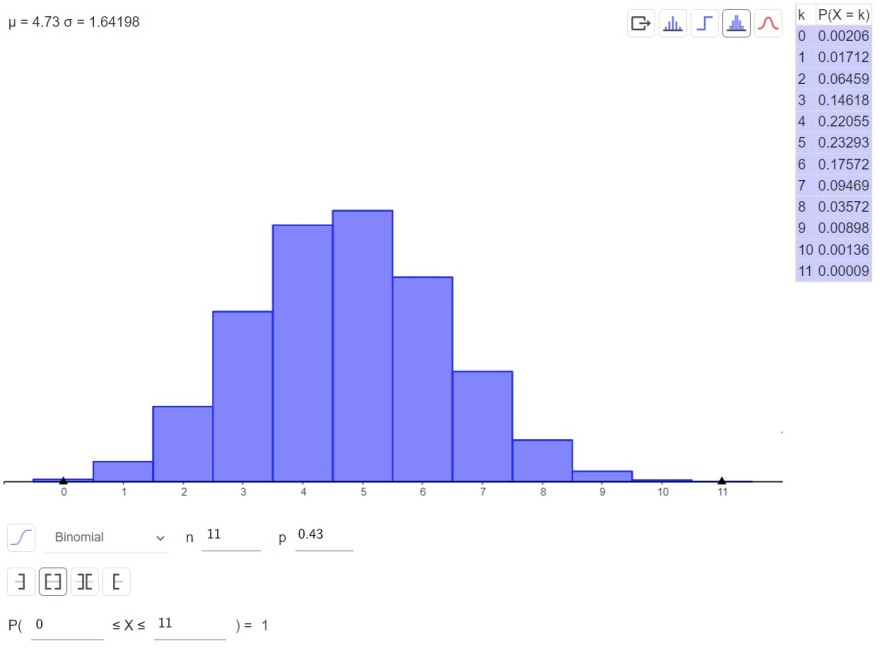
Schau dir die Verteilung für die Anzahl an Treffern an.
Frag dich wann hat man "höchstens 1 Niete". Vermutlich wenn man 10 oder 11 Treffer hat. Also addiert man die Wahrscheinlichkeiten für 10 oder 11 Treffer.
Frag dich, wann hat man mindestens 1 Treffer. Vermutlich wenn man 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 oder 11 Treffer hat. Addiere also alle Wahrscheinlichkeiten. Um Zeit und Arbeit zu sparen kann man auch mit dem Gegenereignis rechnen. Zieh also von 1 die Wahrscheinlichkeit für 0 Treffer ab. Du siehst wie viel einfacher das wird.
Frag dich, wann hat man "weniger als 2 Nieten". Das ist der fall wenn man 0 oder eine Niete hat. Aber moment mal. Das hatten wir ja schon ausgerechnet. Also brauchen wir hier nur die Wahrscheinlichkeit abschreiben.