Aufgabe:

Text erkannt:
Aufgabe 6
Zeigen Sie, dass die folgenden Mengen keine Vektorräume über \( \mathbb{R} \) bilden.
(a) \( V=\mathbb{R}^{3} \) mit \( x+y=\left(\begin{array}{l}x_{1} \\ x_{2} \\ x_{3}\end{array}\right)+\left(\begin{array}{c}y_{1} \\ y_{2} \\ y_{3}\end{array}\right)=\left(\begin{array}{c}x_{1}+y_{1} \\ x_{2}+y_{2} \\ x_{3}+y_{3}\end{array}\right) \) und \( \lambda x=\lambda\left(\begin{array}{l}x_{1} \\ x_{2} \\ x_{3}\end{array}\right)=\left(\begin{array}{c}\lambda x_{1} \\ x_{2} \\ x_{3}\end{array}\right) \)
Problem/Ansatz:
Also ich habe noch Probleme mit dem Verständniss von Vektorräumen und wie ich darauf Prüfe. Habe mich mit mehreren Videos nun zu dieser Lösung hier entlang gehangelt:
Habe erst einmal nach den ganzen Bedingungen geprüft wie:
-(V, (+)) -> Assotiativ
-Neutrale Element von (+)
e = (0,0,0)
-Inverses Element von (+)
v (+) v^-1 = e
-Für Abelsche Gruppe: Kommutativität
v1 (+) v2 = v2 (+) v1
Bis hierhin bin ich zu dem Schluss gekommen, dass diese Bedingungen alle Stimmen. Nun ist mir bei der Distributivität aber eine unregelmäßigkeit aufgefallen:
k (*) ( v1 (+) v2) = k (*) (v1) (+) k (*) (v2)
Da oben in der Aufgabenstellung aber gegeben ist, dass:
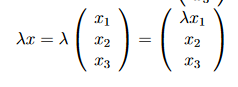
würde ich sagen, dass hier die Distributivität nicht gegeben ist weil das λ lediglich bei dem x1 bleibt aber nicht beim x2 und x3 auftaucht.
Falls das richtig ist und bevor es jetzt heißt "Das hätte man schon schneller erkennen können", ja, mag sein. Ich bin bewusst die einzelnen Schritte durchgegangen um zu sehen ob sich mein Verständniss bei den Schritten auch als Richtig entpuppt hat oder ob ich bereits da Fehler mache.
Bin mir jetzt nicht sicher mit dem Ergebniss...wäre das so legitim?
Beste Grüße,
fvaltrock