a) Zeigen Sie, dass das Schaubild \( \mathrm{K}_{1} \) keine Extrempunkte besizt.
f1(x)= - \( \frac{(x-1)^3}{2} \) Graph:
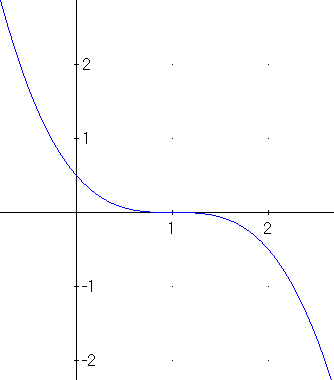
b) In welchem Bereich ist \( K_{1} \) rechtsgekrümmt?
Schau auf den Graphen.
c) Bestimmen Sie für a \( >1 \) die Hoch- und Tiefpunkte von \( \mathrm{K}_{\mathrm{a}} \).
Nullstellen der ersten Ableitung in fa(x) einsetzen. a wie eine Zahl behandeln.
d) Untersuchen Sie, ob es ein a > 1 gibt, so dass die Gerade durch die Extrempunkte eine Parallele zur 1. Winkelhalbierenden ist.
Nimm zwei Punkte aus der Lösung zu c und lege dadurch eine Gerade. Deren Steigung m(a) hängt von a ab. Bestimme a in m(a)=1
e) Für \( a>1 \) bilden die Achsenschnittpunkte von \( \mathrm{K}_{\mathrm{a}} \) ein Dreieck.Skizzieren Sie ein solches Dreieck. Bestimmen Sie einen Wert von a für den dieses Dreieck gleichschenklig ist.
Hier die Graphen für a=2 und a=3:
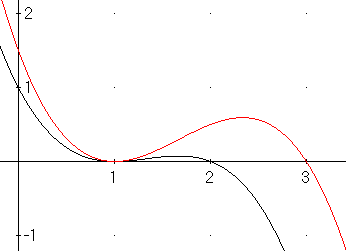
Überlege selbst.
