vektorielles Kurvenintegral berechnen

Question

Aufgabe:

Vektorielles Oberflächenintegral berechnen.

Problem/Ansatz:

Hallo,

mit folgendem habe ich zu kämpfen - ich komme bei diesem Beispiel auf -24pi, was falsch ist. Richtig wäre 2pi(-16+8/3).

Ich finde leider mein Fehler nicht.

Danke und lg

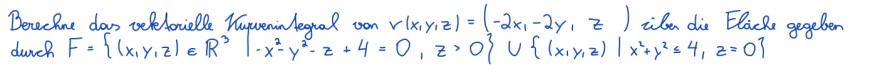
Text erkannt:

Berechne das vetetorielle Knuwenintegral von \( r(x, y, z)=(-2 x,-2 y, z) \) ilber die Eliche gegeben durch \( F=\left\{(x, y, z) \in \mathbb{R}^{3} \mid \cdot x^{2}-y^{2}-z+4=0, z>0\right\} \cup\left\{(x, y, z) \mid x^{2}+y^{2} \leq 4, z=0\right\} \)

Comments

Hallo,

Du hast nicht erwähnt, was mit dem Integral über den Boden ist - dies ist allerdings gleich 0

Ich habe ebenfalls Dein Ergebnis heraus. Würde also mal die Quellen checken:

---

Deine Rechnung stimmt.

Du hast aber übersehen, dass die Menge \(F\) aus zwei Teilemgen besteht. Die erste ist die Mantelfläche \((z>0)\), die zweite ist der Boden \((z=0)\). Da der Normalenvektor des Bodens aber \((0;0;-1)^T\) und \((v_3=z=0)\) ist, verschwindet das Integral über die zweite Fläche.