Text erkannt:
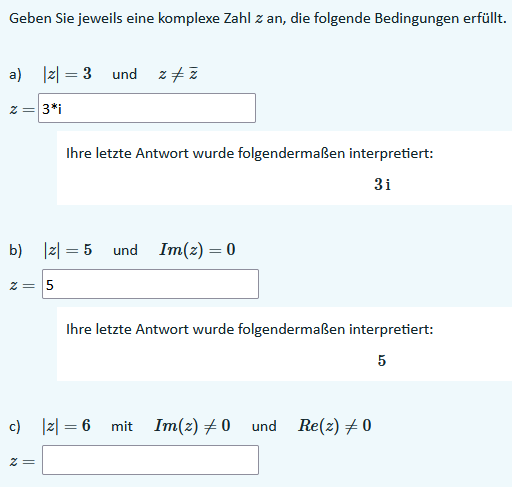
Geben Sie jeweils eine komplexe Zahl z an, die folgende Bedingungen erfüllt.
a) ∣z∣=3 und z=zˉ
z=3∗i
Ihre letzte Antwort wurde folgendermaßen interpretiert:
3i
b) ∣z∣=5 und Im(z)=0
z=5
Ihre letzte Antwort wurde folgendermaßen interpretiert:
5
c) ∣z∣=6 mit Im(z)=0 und Re(z)=0
z=
Aufgabe:
Problem/Ansatz:
Die Lösung ergibt sich doch aus der Formel Re2+Im2
Wie komme ich nun auf die glatte 6 wenn ich Im und Re angeben muss?
Oder ist das überhaupt der richtige Ansatz? Ich komm leider nicht weiter