Permutation, Zyklendarstellung, Signum, Abelsche Gruppen

Question

Wir betrachten die Symmetriegruppe des regelmäßigen 6-Ecks A6. Dabei fassen wir ihre Elemente als Permutationen der gegen den Uhrzeigersinn durchnummerierten Ecken aus B6 auf.

1. Geben Sie für die Permutationen die Zyklendarstellung an!
2. Bestimmen Sie das Signum von den von Ihnen gewählten Permutationen!
3. Begründen Sie, dass A6 nicht abelsch ist, indem sie zwei Permutationen daraus angeben, die in unterschiedlicher Reihenfolge nacheinander ausgeführt unterschiedliche Ergebnisse liefern & geben sie die Ergebnisse ebenfalls an.

Mein Ansatz:

1  2  3  4  5  6
6  5  4  3  2  1

in Zyklendarstellung: (1,6)  (2,5)  (3,4) und als Signum habe ich -1 erhalten

Zum einen weiß ich überhaupt nicht, ob es richtig ist, was ich da getan habe und zum anderen fällt mir die dritte Aufgabe etwas schwer. Ich würde mich über etwas Hilfe freuen und bedanke mich schon mal im Voraus!

Comments

Kann mir keiner helfen? :(

Answer 1

Du hast spiegelungen über die Achsen

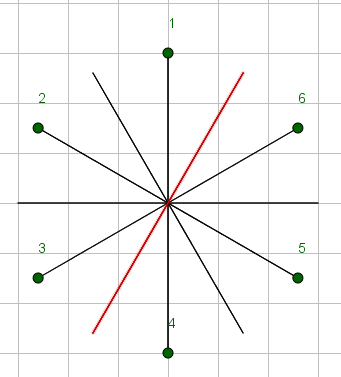
betrachtet - entsprechend der roten Spiegelachse

{6, 5, 4, 3, 2, 1} ==> {{{1, 6}}, {{2, 5}}, {{3, 4}}}

Zykel und Sgn ist korrekt

- ergänze weitere 5 erkennbare spiegelungen

hat ja keiner gesagt alle symmetrien anzugeben