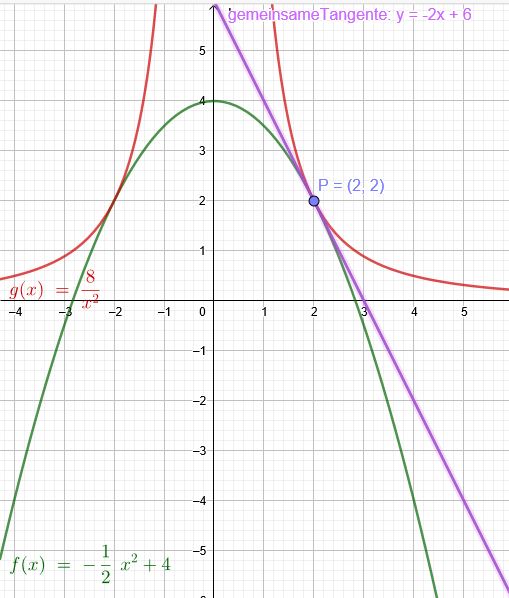
\(f(x)=-a*x^2+b\) und \(g(x)= \frac{c}{x^2} \) berühren sich im Punkt \(P(2|2)\)
\(f(x)=g(x)\)
\(-a*x^2+b=\frac{c}{x^2} |*x^2\)
\(-a*x^4+b*x^2=c\)
\(P(2|2)\)
1.)\(-16a+4b=c\)
\(f(2)=-4a+b\)
2.) \(-4a+b=2\) \(b=2+4a\) ∈ 1.) \(-16a+4*(2+4a)=c\) → \(c=8\)
\(g(x)= \frac{8}{x^2} \)
\(g´(x)= \frac{-16}{x^3} \) \(g´(2)= -2 \)
\(f´(x)=-2a*x\) \(f´(2)=-4a\) \(-4a=-2\) \(a=\frac{1}{2}\)
2.) \(-4*\frac{1}{2}+b=2\) → \(b=4\)
\(f(x)=-\frac{1}{2}*x^2+4\) \(g(x)= \frac{8}{x^2} \)