Aufgabe:
Problem/Ansatz:
Wir betrachten die Reihe
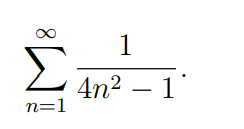
Zeigen Sie, dass für alle n ∈ N die Gleichung
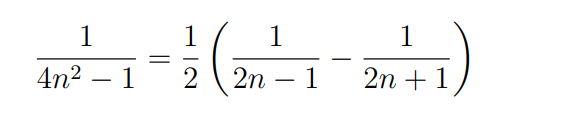
Text erkannt:
\( \frac{1}{4 n^{2}-1}=\frac{1}{2}\left(\frac{1}{2 n-1}-\frac{1}{2 n+1}\right) \)
Text erkannt:
\( \sum \limits_{n=1}^{\infty} \frac{1}{4 n^{2}-1} \)
Hey,
Ich dachte, ich muss überprüfen, ob dies eine Nullsequenz ist. Wenn nicht, divergiert die Serie. Ich wusste nicht, was ich als nächstes tun sollte. Vielen Dank im Voraus für Ihre Hilfe.
