Aufgabe:
Ein Flussgebiet wird immer wieder von Überschwemmungen geplagt, da der Fluss in großen Kurven durch die Landschaft verläuft.
In dem betroffenen Abschnitt lässt sich der Flusslauf näherungsweise durch den Graphen der Funktion f mit f(x) = ×3 - 6 x2 + 9x beschreiben (x und f(x) jeweils in km). Bestimmen Sie den Flächeninhalt des Überschwemmungsgebiets (schraffierte Fläche in
Fig. 1).
b) Ein Ingenieur hat die Idee, den Fluss zu begradigen. Der neue Verlauf lässt sich zwischen den 0 und 2,75 näherungsweise durch den Graphen der Funktion g mit g (x) =-} x? + x beschreiben.
#* beschreiben.
Skizzieren Sie den neuen Verlauf des Flusses. Bestimmen Sie den Inhalt der Fläche, die nun nicht mehr überschwemmt wird.
Problem/Ansatz:
Text erkannt:
\begin{tabular}{l|l|l|l|l}
\( \begin{array}{l}\text { Exponential- und } \\ \text { Logarihmusfunktion } \\ \text { erkennen. }\end{array} \) & & & & \\
\hline \( \begin{array}{l}\text { 11. Ich kann die Produkt- } \\ \text { und Kettenregel zum } \\ \text { Ableiten von Funktionen } \\ \text { anwenden }\end{array} \) & & & & \\
\hline
\end{tabular}
Schlüsselkonzept: Integral
Check-out: Klausurvorbereitung - Test- und Trainingsaufgaben
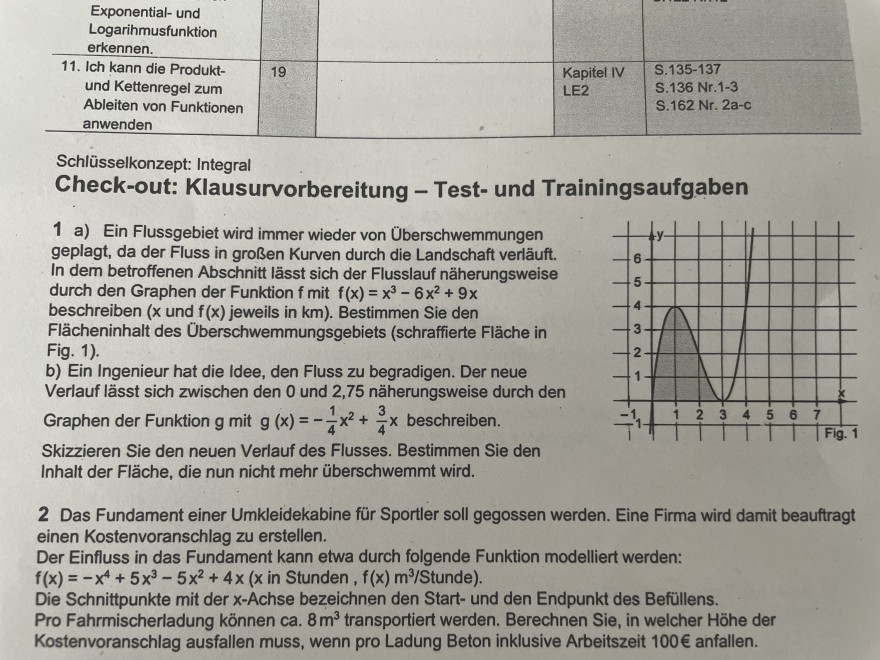
1 a) Ein Flussgebiet wird immer wieder von Überschwemmungen geplagt, da der Fluss in großen Kurven durch die Landschaft verläuft. In dem betroffenen Abschnitt lässt sich der Flusslauf näherungsweise durch den Graphen der Funktion \( f \) mit \( f(x)=x^{3}-6 x^{2}+9 x \) beschreiben \( (x \) und \( f(x) \) jeweils in \( k m \) ). Bestimmen \( S i e \) den Flächeninhalt des Überschwemmungsgebiets (schraffierte Fläche in Fig. 1).
b) Ein Ingenieur hat die Idee, den Fluss zu begradigen. Der neue Verlauf lässt sich zwischen den 0 und 2,75 näherungsweise durch den Graphen der Funktion \( g \) mit \( g(x)=-\frac{1}{4} x^{2}+\frac{3}{4} x \) beschreiben.
Skizzieren Sie den neuen Verlauf des Flusses. Bestimmen Sie den Inhalt der Fläche, die nun nicht mehr überschwemmt wird.
2 Das Fundament einer Umkleidekabine für Sportler soll gegossen werden. Eine Firma wird damit beauftragt einen Kostenvoranschlag zu erstellen.
Der Einfluss in das Fundament kann etwa durch folgende Funktion modelliert werden: \( f(x)=-x^{4}+5 x^{3}-5 x^{2}+4 x\left(x\right. \) in Stunden, \( f(x) m^{3} / S \) tunde \( ) \).
Die Schnittpunkte mit der \( x \)-Achse bezeichnen den Start- und den Endpunkt des Befüllens.
Pro Fahrmischerladung können ca. \( 8 \mathrm{~m}^{3} \) transportiert werden. Berechnen Sie, in welcher Höhe der Kostenvoranschlag ausfallen muss, wenn pro Ladung Beton inklusive Arbeitszeit \( 100 € \) anfallen.

Text erkannt:
Schlüsselkonzept: Integral
Check-out: Klausurvorbereitung - Test- und Trainingsaufgaben
1 a) Ein Flussgebiet wird immer wieder von Überschwemmungen geplagt, da der Fluss in großen Kurven durch die Landschaft verläuft. In dem betroffenen Abschnitt lässt sich der Flusslauf näherungsweise durch den Graphen der Funktion \( f \) mit \( f(x)=x^{3}-6 x^{2}+9 x \) beschreiben \( (x \) und \( f(x) \) jeweils in \( \mathrm{km} \) ). Bestimmen Sie den Flächeninhalt des Überschwemmungsgebiets (schraffierte Fläche in Fig. 1).
b) Ein Ingenieur hat die Idee, den Fluss zu begradigen. Der neue Verlauf lässt sich zwischen den 0 und 2,75 näherungsweise durch den Graphen der Funktion \( g \) mit \( g(x)=-\frac{1}{4} x^{2}+\frac{3}{4} x \) beschreiben.
Skizzieren Sie den neuen Verlauf des Flusses. Bestimmen Sie den Inhalt der Fläche, die nun nicht mehr überschwemmt wird.
2 Das Fundament einer Umkleidekabine für Sportler soll gegossen werden. Eine Firma wird damit beauftragt einen Kostenvoranschlag zu erstellen.
Der Einfluss in das Fundament kann etwa durch folgende Funktion modelliert werden:
\( f(x)=-x^{4}+5 x^{3}-5 x^{2}+4 x\left(x\right. \) in Stunden, \( f(x) m^{3} / \) Stunde).
Die Schnittpunkte mit der \( x \)-Achse bezeichnen den Start- und den Endpunkt des Befüllens.
Pro Fahrmischerladung können ca. \( 8 \mathrm{~m}^{3} \) transportiert werden. Berechnen Sie, in welcher Höhe der Kostenvoranschlag ausfallen muss, wenn pro Ladung Beton inklusive Arbeitszeit \( 100 € \) anfallen.
3 Bestimmen Sie den Flächeninhalt der von den Graphen von \( f \) und \( g \) begrenzt wird.
\( f(x)=\frac{-1}{2} x^{2}+2 x+3 ; g(x)=\frac{1}{2}(x-4)^{2}+2(x-4)+3 \)