F(x), Funktion, Log Log Plot

Question

Aufgabe:

F(x), Funktion, Log Log Plot

Problem/Ansatz:

Ich habe einen Gas Sensor und möchte den PPM wert ermitteln.

Hier die webseite dazu. https://www.teachmemicro.com/use-mq-7-carbon-monoxide-sensor/

Es ist soweit alles verständlich aber ich brauche Hilfe bei der letzen Zeile.

ppm = (1538,46\( \frac{RS}{R0} \))^-1.709

Wie kommt man auf die 1538,46 ??

Lg Sebastian

Text erkannt:

\( F(x)=F_{0}\left(\frac{x}{x_{0}}\right)^{\frac{\log \left(F_{1} / F_{0}\right)}{\log \left(x_{1} / x_{0}\right)}} \)
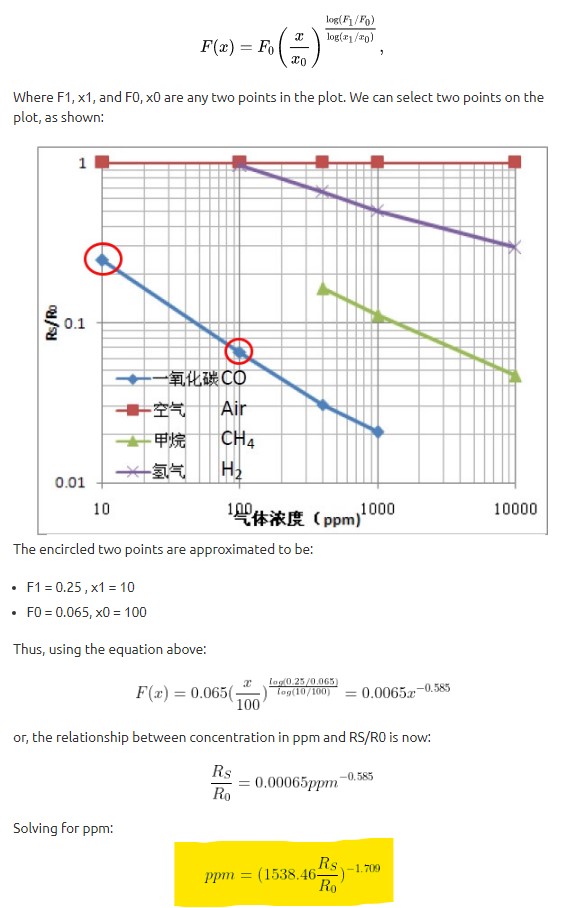
Where \( F 1, x 1 \), and F0, \( x 0 \) are any two points in the plot. We can select two points on the plot, as shown:
The encircled two points are approximated to be:
- \( F 1=0.25, x 1=10 \)
- \( F 0=0.065, x 0=100 \)
Thus, using the equation above:
\( F(x)=0.065\left(\frac{x}{100}\right)^{\frac{\operatorname{logog}(0.25 / 0.065)}{\log (10 / 100)}}=0.0065 x^{-0.585} \)
or, the relationship between concentration in \( \mathrm{ppm} \) and \( \mathrm{RS} / \mathrm{RO} \) is now:
\( \frac{R_{S}}{R_{0}}=0.00065 \mathrm{ppm}^{-0.585} \)
Solving for \( \mathrm{ppm} \) :
\( p p m=\left(1538.46 \frac{R_{S}}{R_{0}}\right)^{-1.709} \)

Answer 1

Man teilt durch 0,00065.

Man nimmt dann beide Seiten hoch \( -\frac{1}{0,585} \).

Wenn man sich die Lösung anschaut, scheint \( -\frac{1}{0,585} \) näherungsweise -1,709 zu sein.

Comments

Danke für deine schnelle Antwort.

Ich hab das noch immer nicht ganz verstanden wie man auf die 1538,46 kommt.

Kannst du mir das bitte nocheinmal mit kompletten Rechenweg erklären?

Vielen Dank abakus.

Lg

---

Ich habe dir den kompletten Rechenweg erklärt. Er besteht aus zwei Rechenbefehlen. Nimm zum Nachvollziehen einen Taschenrechner.

---

was muss ich durch 0,00065 teilen?

---

Wie man das mit Rechenbefehlen so macht: Man wendet sie auf beiden Seiten der Gleichung an. Aber mach dir jetzt noch keine Sorgen. Das lernt ihr erst in der 7. Klasse.

---

Wieso ist es nicht möglich einfsach die Rechnung hinzuschreiben.

Ich weiß nicht was du meinst mit Rechenbefehlen und auf beiden seiten hoch nehmen.

Ich bräuchte bitte den kompletten rechenweg mit eingestzen zahlen.

Das ist doch ein Matheforum oder?

---

Die Gleichung

\( \frac{R_{S}}{R_{0}}=0.00065 \mathrm{ppm}^{-0.585} \)

hattest du noch nicht gelb markiert. Ich gehe deshalb davon aus, dass es dir um die Umwandlung(en) zwischen dieser Zeile und der nächsten Zeile geht.

Also erster Schritt:

Teile beide Seiten der Gleichung

\( \frac{R_{S}}{R_{0}}=0.00065 \mathrm{ppm}^{-0.585} \)

durch 0,00065.

Was erhältst du daraus als neue Gleichung?

---

Also ich hätte dann

\( \frac{RS}{R0} \) / 0,00065 = \( x^{0,00065·-0,585} \) / 0,00065

aber egal wie ich es drehe und wende auf meinem Taschenrechner bekomme ich nie die Zahl 1538,46 zu sehen

Mir geht es rein darum warum da die Zahl 1538,46 steht.

Danke Dir

---

bekomme ich nie die Zahl 1538,46 zu sehen

Also wenn ICH 1/0,00065 rechnen lasse, bekomme ICH rund 1538,46 zu sehen.

---

Jetz haben wir es.

Asoo weil ja \( \frac{RS}{R0} \) gleich 1 ist.

Ich bin ein Trottel :-)

Vielen vielen Dank !!

Schönes Wochenende !!

---

Asoo weil ja \( \frac{RS}{R0} \) gleich 1 ist.

NEIN! Das hat niemand behauptet.

Die Gleichung \( \frac{R_{S}}{R_{0}}=0.00065 \mathrm{ppm}^{-0.585} \)

lässt sich schreiben als

\( \pink{1\cdot}\frac{R_{S}}{R_{0}}=0.00065 \mathrm{ppm}^{-0.585} \).

Und DAS kannst du jetzt durch durch 0,00065. teilen.