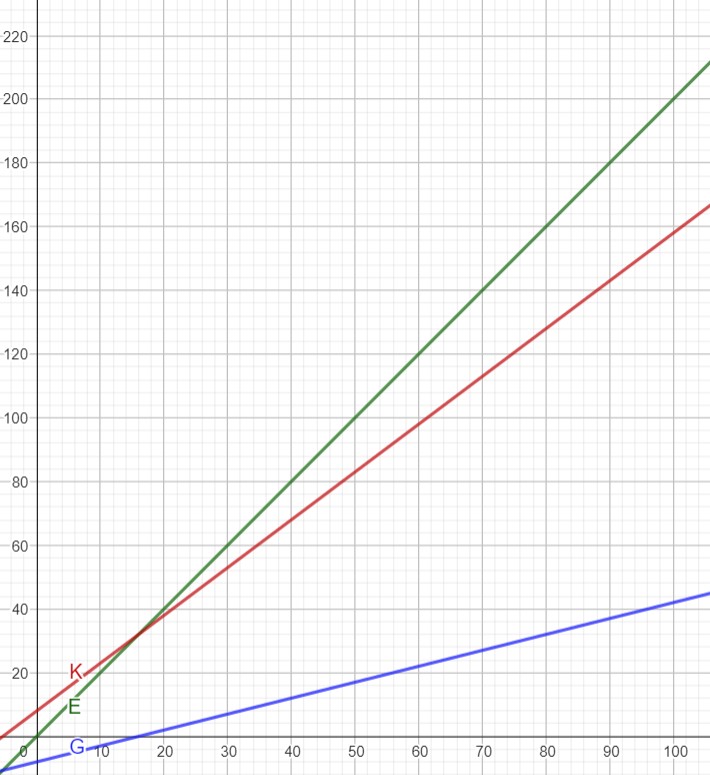
Wo liegen denn genau deine Probleme. Die Erlösfunktion ist eine Funktion der Form
E(x) = m·x
Wenn diese durch den Punkt (10 | 20) geht solltest du sie Aufstellen können. Die Kostenfunktion ist eine Funktion der Form
K(x) = m·x + b
Diese Funktion geht durch die Punkte (0 | 8) und (10 | 23). Hiermit sollte es auch möglich sein die Funktion aufzustellen.
Wenn du jetzt noch weißt, dass sich der Gewinn aus Erlös minus Kosten berechnet sollteest du auch in der Lage sein die Gewinnfunktion aufzustellen. Zeichne dann auch alle Funktionen in ein Koordinatensystem ein.
Das könnte dann wie folgt aussehen