Hallo,
du bestimmst zunächst die Vektoren, die den Winkel einschließen.
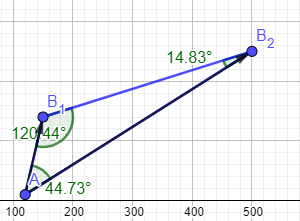
\(\vec{a}=\overrightarrow{AB_1}=\begin{pmatrix} 150-120\\140-10\\ \end{pmatrix}=\begin{pmatrix} 30\\130 \end{pmatrix}\\ \vec{b}=\overrightarrow{AB_2}=\begin{pmatrix} 380\\240 \end{pmatrix}\)
Dann setzt du die Werte in die Formel ein
\(cos(\alpha)=\frac{\begin{pmatrix} 30\\130 \end{pmatrix}\circ\begin{pmatrix} 380\\240 \end{pmatrix}}{\sqrt{30^2+130^2}\cdot \sqrt{380^2+240^2}}=\frac{42600}{10\sqrt{178\cdot 20\sqrt{505}}}=0,710434287\\ cos^{-1}(0,710434287)=44,73°\)
Den 2. Winkel berechnest du auf die gleiche Weise.
Gruß, Silvia